–†–µ—И–µ–љ–Є–µ:
1. –°–Њ—Б—В–∞–≤–Є–Љ –Є–љ—В–µ—А–≤–∞–ї—М–љ—Л–є —А—П–і —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –і–ї—П –≤—Л–±–Њ—А–Ї–Є :
–∞) —Г–њ–Њ—А—П–і–Њ—З–Є–Љ –Ј–љ–∞—З–µ–љ–Є—П –≤—Л–±–Њ—А–Ї–Є –њ–Њ –≤–Њ–Ј—А–∞—Б—В–∞–љ–Є—О:
5 5 6 6 7 7 7 7 8 8 8 9 9 9 9 10 10 10 10 10
- –љ–∞–є–і–µ–Љ –і–Є–∞–њ–∞–Ј–Њ–љ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –њ—А–Є–Ј–љ–∞–Ї–∞ x (—А–∞–Ј–Љ–∞—Е –≤—Л–±–Њ—А–Ї–Є)
–Я—Г—Б—В—М \(x_{min}\) –Є \(x_{max}\) − —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –љ–∞–Є–Љ–µ–љ—М—И–µ–µ –Є –љ–∞–Є–±–Њ–ї—М—И–µ–µ –Ј–љ–∞—З–µ–љ–Є—П –≤–∞—А–Є–∞–љ—В –≤—Л–±–Њ—А–Ї–Є. –Т–µ–ї–Є—З–Є–љ–∞
\(R = x_{max} - x_{min} = 10-5=5\) –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —А–∞–Ј–Љ–∞—Е–Њ–Љ –≤—Л–±–Њ—А–Ї–Є
–±) –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤
–Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ –Њ–і–љ–Њ–є –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е —Д–Њ—А–Љ—Г–ї
\(K \approx \sqrt{n} \approx \sqrt{20} => K = 5 \).
\(K < 5\lg(20) => K < 6.5 \).
–Ь–Њ–ґ–љ–Њ –њ–Њ–ї—М–Ј–Њ–≤–∞—В—М—Б—П –Є –і—А—Г–≥–Є–Љ–Є —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–Є–Љ–Є —Д–Њ—А–Љ—Г–ї–∞–Љ–Є, –љ–∞–њ—А–Є–Љ–µ—А, —Д–Њ—А–Љ—Г–ї–Њ–є –°—В–µ—А–і–ґ–µ—Б–∞
\(K \approx 1пАЂ + 3.322 \ln(n) => K \approx 1пАЂ + 3.322 \lg(20) => K = 5 \).
–Ю–Ї—А—Г–≥–ї—П–µ–Љ —А–µ–Ј—Г–ї—М—В–∞—В –і–Њ —Ж–µ–ї–Њ–≥–Њ —З–Є—Б–ї–∞.
–≠—В–Є —Д–Њ—А–Љ—Г–ї—Л –і–∞—О—В –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї—М–љ–Њ —А–∞–≤–љ—Л–µ —А–µ–Ј—Г–ї—М—В–∞—В—Л.
–Ю–±—Л—З–љ–Њ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—О—В, —З—В–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ –і–Њ–ї–ґ–љ–Њ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П—В—М —Г—Б–ї–Њ–≤–Є—О \(5 \leq K \leq 20 \).
–≤) –љ–∞–є–і–µ–Љ —И–Є—А–Є–љ—Г –Є–љ—В–µ—А–≤–∞–ї–∞
\(d = \frac{R}{K} = \frac{5}{5}=1\)
–≥) –°–Њ—Б—В–∞–≤–Є–Љ —В–∞–±–ї–Є—Ж—Г –Є–љ—В–µ—А–≤–∞–ї—М–љ–Њ–є –≥—А—Г–њ–њ–Є—А–Њ–≤–Ї–Є, –Ї–Њ—В–Њ—А–∞—П –±—Г–і–µ—В –≤—Л–≥–ї—П–і–µ—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
–Я–Њ—Б–ї–µ —А–∞–Ј–±–Є–µ–љ–Є—П –љ–∞ –Є–љ—В–µ—А–≤–∞–ї—Л –Њ–њ—А–µ–і–µ–ї—П—О—В:
- –∞–±—Б–Њ–ї—О—В–љ—Л–µ —З–∞—Б—В–Њ—В—Л \(m_i\) , i=1,..,K , –≥–і–µ \(m_i\) − –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –≤—Л–±–Њ—А–Ї–Є, –њ–Њ–њ–∞–≤—И–Є—Е –≤ i − –є –Є–љ—В–µ—А–≤–∞–ї (—Н–ї–µ–Љ–µ–љ—В, –њ–Њ–њ–∞–≤—И–Є–є –љ–∞ –≥—А–∞–љ–Є—Ж—Г –Є–љ—В–µ—А–≤–∞–ї–∞, –Њ—В–љ–Њ—Б—П—В –Ї –Ї–∞–Ї–Њ–Љ—Г-–љ–Є–±—Г–і—М –≤—Л–±—А–∞–љ–љ–Њ–Љ—Г –Є–љ—В–µ—А–≤–∞–ї—Г, –љ–∞–њ—А–Є–Љ–µ—А, –ї–µ–≤–Њ–Љ—Г, –Є–ї–Є –њ—А–∞–≤–Њ–Љ—Г; –µ—Б–ї–Є –љ–∞ –≥—А–∞–љ–Є—Ж—Г –Є–љ—В–µ—А–≤–∞–ї–∞ –њ–Њ–њ–∞–і–∞–µ—В –Љ–љ–Њ–≥–Њ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –≤—Л–±–Њ—А–Ї–Є, —В–Њ –Є—Е –і–µ–ї—П—В –њ–Њ–њ–Њ–ї–∞–Љ –Љ–µ–ґ–і—Г –ї–µ–≤—Л–Љ –Є –њ—А–∞–≤—Л–Љ –Є–љ—В–µ—А–≤–∞–ї–∞–Љ–Є);
- –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Л–µ —З–∞—Б—В–Њ—В—Л \(h_i = \frac{m_i}{n}\)
- –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Л–µ –љ–∞–Ї–Њ–њ–ї–µ–љ–љ—Л–µ —З–∞—Б—В–Њ—В—Л \( \sum_{j=1}^i\frac{m_j}{n} = \sum_{j=1}^ih_j, \quad i = 1,2,...K\)
- —Б–µ—А–µ–і–Є–љ—Л –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ \(u_i\)
$$\begin{array}{|c|c|}–Ш–љ—В–µ—А–≤–∞–ї—Л & 5-6 & 6-7 & 7-8 & 8-9 & 9-10 & 10-11\\ —З–∞—Б—В–Њ—В—Л(m_i) & 2 & 2 & 4 & 3 & 4 & 5 \\ –Њ—В–љ–Њ—Б. —З–∞—Б—В–Њ—В—Л(h_i) & 0.1 & 0.1 & 0.2 & 0.15 & 0.2 & 0.25 \\ –Њ—В–љ–Њ—Б.–љ–∞–Ї–Њ–њ.—З–∞—Б—В & 0.1 & 0.2 & 0.4 & 0.55 & 0.75 & 1\\ u_i & 5.5 & 6.5 & 7.5 & 8.5 & 9.5 & 10.5\end{array}$$
- –Я—А–Є —Н—В–Њ–Љ \( \sum_{i=1}^Km_i =n; \quad \sum_{i=1}^Kh_i=1\)
2. –љ–∞–є—В–Є —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї—Г—О —Д—Г–љ–Ї—Ж–Є—О –Є –њ–Њ—Б—В—А–Њ–Є—В—М –µ–µ –≥—А–∞—Д–Є–Ї:
–≠–Љ–њ–Є—А–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П (—Д—Г–љ–Ї—Ж–Є–µ–є —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤—Л–±–Њ—А–Ї–Є) –љ–∞–Ј—Л–≤–∞—О—В —Д—Г–љ–Ї—Ж–Є—О \(F(x)\), –Њ–њ—А–µ–і–µ–ї—П—О—Й—Г—О –і–ї—П –Ї–∞–ґ–і–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П \(x\) –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Г—О —З–∞—Б—В–Њ—В—Г —Б–Њ–±—Л—В–Є—П \(X < x\): $$F(x) = \frac{n_x}{n}$$
\(n_x\) — —З–Є—Б–ї–Њ –≤–∞—А–Є–∞–љ—В, –Љ–µ–љ—М—И–Є—Е \(x\); \(n\) — –Њ–±—К–µ–Љ –≤—Л–±–Њ—А–Ї–Є.
–≠–Љ–њ–Є—А–Є—З–µ—Б–Ї—Г—О —Д—Г–љ–Ї—Ж–Є—О —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П \(F_n(x)\) –њ–Њ–ї—Г—З–∞—О—В –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ–Љ —Б—В—Г–њ–µ–љ—З–∞—В–Њ–є –Ї—А–Є–≤–Њ–є –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Л—Е –љ–∞–Ї–Њ–њ–ї–µ–љ–љ—Л—Е —З–∞—Б—В–Њ—В; \(F_n(x)\) –Є–Љ–µ–µ—В —Б–Ї–∞—З–Ї–Є –≤ —В–Њ—З–Ї–∞—Е, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е —Б–µ—А–µ–і–Є–љ–∞–Љ –Є–љ—В–µ—А–≤–∞–ї–Њ–≤ \(u_i\) .
–Э–∞–є–і–µ–Љ —Н–Љ–њ–Є—А–Є—З–µ—Б–Ї—Г—О —Д—Г–љ–Ї—Ж–Є—О
–Э–∞–Є–Љ–µ–љ—М—И–∞—П –≤–∞—А–Є–∞–љ—В–∞ —А–∞–≤–љ–∞ 5, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ F(x)=0 –њ—А–Є \( x \leq 5\) . –Ч–љ–∞—З–µ–љ–Є–µ \( —Е < 6\) , –∞ –Є–Љ–µ–љ–љ–Њ \( F(x)=h_1= 0.1\), –њ—А–Є \(x < 6; h_1=0.1;h_2=0.1 => F(x) = h_1+h_2=0.2\) –Є —В.–і. $$F(x) = \begin{cases} 0 & x < 5\\ 0.1 & 5 \leq x < 6 \\ 0.2 & 6 \leq x < 7 \\ 0.4 & 7 \leq x < 8 \\ 0.55 & 8 \leq x < 9 \\ 0.75 & 9 \leq x < 10 \\ 1 & 10 \leq x \end{cases}$$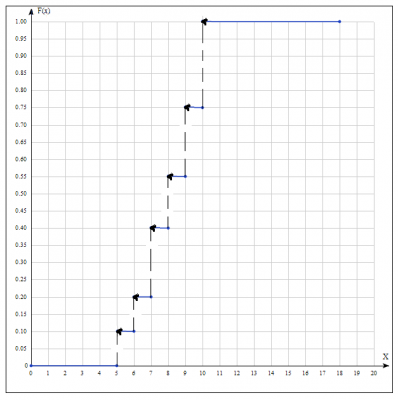
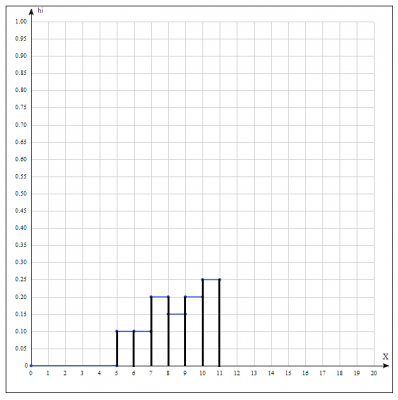
3. –њ–Њ—Б—В—А–Њ–Є—В—М –≥–Є—Б—В–Њ–≥—А–∞–Љ–Љ—Г —З–∞—Б—В–Њ—В:
–і–∞–љ–љ—Л–µ –±–µ—А–µ–Љ –Є–Ј —В–∞–±–ї–Є—Ж—Л
4. –љ–∞–є—В–Є —Б—А–µ–і–љ–Є–є –і–Њ—Е–Њ–і –њ—А–µ–і–њ—А–Є—П—В–Є—П (–≤—Л–±–Њ—А–Њ—З–љ—Г—О —Б—А–µ–і–љ—О—О), –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –Њ—В —Б—А–µ–і–љ–µ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П –њ—А–Є–±—Л–ї–Є (–і–Є—Б–њ–µ—А—Б–Є—О –Є —Б—А–µ–і–љ–µ–µ –Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ).
- –Т—Л–±–Њ—А–Њ—З–љ–∞—П —Б—А–µ–і–љ—П—П, –µ—Б–ї–Є —Б–і–µ–ї–∞–љ–∞ –і–Є—Б–Ї—А–µ—В–љ–∞—П –≥—А—Г–њ–њ–Є—А–Њ–≤–Ї–∞ —А–∞—Б—Б—З–Є—В—Л–≤–∞–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$\overline{x} = \frac{1}{n}\sum_{i=1}^Km_ix_i = \sum_{i=1}^Kh_ix_i$$
–°—З–Є—В–∞–µ–Љ $$\overline{x} = 5*0.1+6*0.1+7*0.2+8*0.15+9*0.2+10*0.25 = 8$$
–Ь–Њ–ґ–љ–Њ –±—Л–ї–Њ —А–∞—Б—Б—З–Є—В–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$\overline{x} = \frac{1}{n}\sum_{i=1}^nx_i$$ $$ \overline{x} = \frac{1}{20}(5+ 5+ 6+ 6+ 7+ 7+ 7+ 7+ 8+ 8+ 8+ 9+ 9+ 9+ 9+ 10+ 10+ 10+ 10+ 10) = \frac{160}{20}=8$$
− –≤—Л–±–Њ—А–Њ—З–љ–∞—П (—Н–Љ–њ–Є—А–Є—З–µ—Б–Ї–∞—П) –і–Є—Б–њ–µ—А—Б–Є—П
$$ \sigma = S^2 = \frac{1}{n-1}\sum_{i=1}^Km_i(x_i-\overline{x})^2 = $$$$ \sigma= \frac{1}{20-1}[2(5-8)^2+2(6-8)^2+4(7-8)^2+3(8-8)^2+4(9-8)^2+5(10-8)^2] \approx 2.84$$
- —Б—А–µ–і–љ–µ–µ –Ї–≤–∞–і—А–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ
$$S = \sqrt{\sigma} = \sqrt{2.84} = 1.69$$



