Решение:
1) составить дискретное (точечное) статистическое распределение;
Проведем группировку по отдельным значениям признака, то есть по стоимости товара (дискретная группировка):
а) выписываем разные значения вариант, попавших в выборку, упорядочим полученные значения по возрастанию:
5 6 7 8 9 10 11 14 15 16 17 19
Получили дискретный вариационный ряд.
б) рассчитываем частоту каждой варианты из вариационного ряда, заносим данные в таблицу - получили дискретное статистическое распределение.
После группировки по значениям определяем:
- абсолютные частоты \(m_i\) , i=1,..,K , где \(m_i\) − количество одинаковых элементов выборки
- относительные частоты \(h_i = \frac{m_i}{n}\)
- относительные накопленные частоты \( \sum_{j=1}^i\frac{m_j}{n} = \sum_{j=1}^ih_j, \quad i = 1,2,...K\)
$$\begin{array}{|c|c|} x_i & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 14 & 15 & 16 & 17 & 19 & \sum\\ m_i & 2 & 1 & 2 & 1 & 2 & 2 & 2 & 2 & 2& 1 & 1 & 2 & 20\\ h_i & 0.1 & 0.05 & 0.1 & 0.05 & 0.1 & 0.1 & 0.1 & 0.1 & 0.1 & 0.05 & 0.05 & 0.1 & 1 \\ s_i=\sum_{j=1}^i\frac{m_j}{n} & 0.1 & 0.15 & 0.25 & 0.3 & 0.4 & 0.5 & 0.6 & 0.7 & 0.8 & 0.85 & 0.9 & 1\end{array}$$
2) найти эмпирическую функцию и построить ее график;
Эмпирической функцией распределения (функцией распределения выборки) называют функцию \(F(x)\), определяющую для каждого значения \(x\) относительную частоту события \(X < x\): $$F(x) = \frac{n_x}{n}$$ \(n_x\) — число вариант, меньших \(x\); \(n\) — объем выборки. Эмпирическую функцию распределения \(F_n(x)\) получают построением ступенчатой кривой относительных накопленных частот; \(F_n(x)\) имеет скачки в точках, соответствующих серединам интервалов \(u_i\) . Найдем эмпирическую функцию 1. Наименьшая варианта равна 5, следовательно F(x)=0 при \( x \leq 5\).
2. При значении \( 5 \leq x < 6\) , \( F(x)=0+ h_1= 0.1 = s_1\)
3. При значении \( 6 \leq x < 7\) , \( F(x)= 0+h_1+h_2= 0+0.1+0.05 = 0.15 =s_2\)
4. При значении \( 7 \leq x < 8\) , \( F(x)= 0+h_1+h_2+h_3= 0+0.1+0.05+0.1 = 0.25 =s_3\) и т.д. $$F(x) = \begin{cases} 0 & x < 5\\ 0.1 & 5 \leq x < 6 \\ 0.15 & 6 \leq x < 7 \\ 0.25 & 7 \leq x < 8 \\ 0.3 & 8 \leq x < 9 \\ 0.4 & 9 \leq x < 10 \\ 0.5 & 10 \leq x < 11 \\ 0.6 & 11 \leq x < 14 \\ 0.7 & 14 \leq x < 15 \\ 0.8 & 15 \leq x < 16 \\ 0.85 & 16 \leq x < 17 \\ 0.9 & 17 \leq x < 19 \\ 1 & 19 \leq x \end{cases}$$
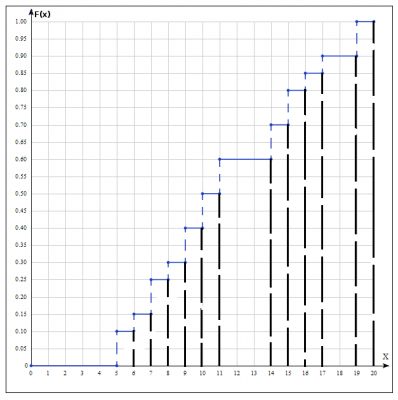
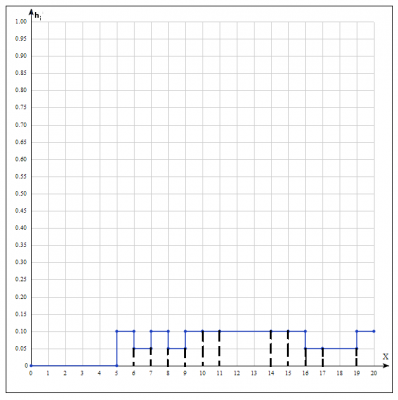
3) построить полигон относительных частот;
данные берем из таблицы
4. найти средний доход предприятия (выборочную среднюю), отклонения от среднего значения прибыли (дисперсию и среднее квадратическое отклонение).
- Выборочная средняя, если сделана дискретная группировка рассчитывается по формуле $$\overline{x} = \frac{1}{n}\sum_{i=1}^Km_ix_i = \sum_{i=1}^Kh_ix_i$$
Считаем $$\overline{x} = 5*0.1+6*0.05+7*0.1+8*0.05+9*0.1+10*0.1+11*0.1+$$$$+14*0.1+15*0.1+16*0.05+17*0.05+19*0.1 = 11.35$$
Можно было рассчитать по формуле $$\overline{x} = \frac{1}{n}\sum_{i=1}^nx_i$$ $$ \overline{x} = \frac{1}{20}(11+ 7+ 7+ 15+ 14+ 9+ 19+ 11+ 5+ 6+ 14+ 16+$$$$+ 8+ 5+ 19+ 17+ 15+ 10+ 10+ 9) = \frac{227}{20}=11.35$$
− выборочная (эмпирическая) дисперсия
$$ \sigma = S^2 = \frac{1}{n-1}\sum_{i=1}^Km_i(x_i-\overline{x})^2 = $$$$ \sigma= \frac{1}{20-1}[2(5-11.35)^2+1(6-11.35)^2+2(7-11.35)^2+1(8-11.35)^2+$$$$+2(9-11.35)^2+2(10-11.35)^2+2(11-11.35)^2+2(14-11.35)^2+2(15-11.35)^2+$$$$+1(16-11.35)^2+1(17-11.35)^2+2(19-11.35)^2] \approx 20.24$$
- среднее квадратическое отклонение
$$S = \sqrt{\sigma} = \sqrt{20.24} \approx 4.5$$



