Решение: найдем максимальное значение функции \(f (x, y)\)
Алгоритм решения задачи "геометрическая интерпретация задачи нелинейного программирования":
1. Строим область допустимых решений задачи \(D\).
Областью \(D\) является четырехугольник \(OABC\) см. рис.
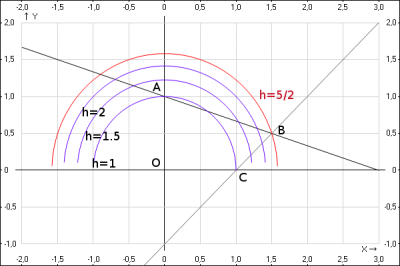
2. Анализ рисунка.
Пусть значение целевой функции равно \(f(x;y) = x^2+y^2 = h\), получаем линии уровня - окружности \(x^2+y^2=h\) - окружность с центром \(O(0;0)\) и радиусом \(R = \sqrt{h}\). С увеличение (уменьшением) числа \(h\) значения функции \(F\) соответственно увеличиваются (уменьшаются). Проводя из точки \(O\) окружности разных радиусов, видим, что целевая функция принимает максимальное значение в точке \(B\).
3. Находим максимальное значение целевой функции.
Найдем координаты точки \(B\) - точки пересечения прямых \(x+3y=3;\quad x-y=1\) путем решения системы уравнений $$\begin{cases} x+3y=3 \\ x-y=1 \end{cases} =>\begin{cases} 1+y+3y=3 \\ x=1+y \end{cases} =>\begin{cases} y=\frac{1}{2} \\ x=\frac{3}{2} \end{cases}$$ Подставляем полученные координаты в целевую функцию и получаем максимальное значение $$f_{max} = (\frac{1}{2})^2+ (\frac{3}{2})^2 = \frac{5}{2}$$
Ответ: максимальное значение функции \(f_{max} = \frac{5}{2}\)



