Решение: в задании говориться о нахождении наибольшей ! площади, т.е. нужно найти экстремум функции. Рассмотрим формулу площади прямоугольника \(S = ab\), где a,b - стороны прямоугольника. Найдем стороны прямоугольника, для этого рассмотрим рисунок.
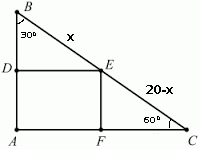
Согласно условия задачи угол \(\angle C = 60^0\). Воспользуемся свойством треугольника - сумма углов треугольника равна \(\angle A + \angle B + \angle C = 180^0 => 90^0+ \angle B + 60^0 = 180^0 => \angle B = 30^0\)
Введем обозначения: пусть точка E делит гипотенузу на два отрезка, т.е. \(BE+EC=20\), тогда обозначим \(BE = x\) тогда \(EC = 20 -x \).
Рассмотрим треугольник \(ΔDBE\), это прямоугольный треугольник, угол \( \angle B =30^0\). Катет лежащий напротив угла в \(30^0\) в два раза меньше гипотенузы \(DE = BE*\sin(30^0) = \frac{1}{2}BE = \frac{1}{2}x\).
Рассмотрим треугольника \(ΔFEC\) получаем \(EF = EC*\sin(60^0) = \frac{\sqrt{3}}{2}(20-x)\).
Площадь прямоугольника равна $$S = DE*EF = \frac{1}{2}x*\frac{\sqrt{3}}{2}(20-x) = \frac{\sqrt{3}}{4}x(20-x)$$ Получили площадь треугольника как функцию одной переменной \(S(x)\) теперь можно искать экстремум функции.
Для нахождения экстремума максимума функции найдем первую производную и приравняем ее у нулю $$s' = (\frac{\sqrt{3}}{4}x(20-x))' = (\frac{\sqrt{3}}{4}(20x-x^2))' = \frac{\sqrt{3}}{4}(20-2x)$$ приравняем производную к нулю $$ s' = \frac{\sqrt{3}}{4}(20-2x) = 0 => 20 - 2x = 0 => x=10$$ функция имеет одну стационарную точку \(x=10\). Уравнение площади прямоугольника \(S(x) = \frac{1}{4}x(20-x) = 5x-\frac{1}{4}x^2\) - парабола, ветви которой направлены вниз (минус перед \(x^2\)), т.е. полученная точка \(x=10\) - это точка максимума и дальнейшие исследования на экстремум проводить не нужно.
Найдем стороны прямоугольника:
\(DE = \frac{1}{2}x = \frac{1}{2}*10=5\)
\(EF = \frac{\sqrt{3}}{2}(20-x) = \frac{\sqrt{3}}{2}(20-10) = 5\sqrt{3}\)
Ответ: для того, чтобы площадь треугольника была наибольшей, его размеры должны быть равны \(DE = 5 \quad EF = 5\sqrt{3}\)





