Решение:
Если подынтегральная функция \(f(x;y)\) отождествляется с поверхностной плотностью \( \mu(x;y)\) пластины, которая занимает область \(D\) в плоскости xOy, тогда масса материальной пластины определяется по формуле $$ m = \int\int_D \mu(x;y)dxdy \quad (1)$$
Алгоритм нахождения массы материальной пластины
1. Рассмотрим плоскость \(D\).
Плоскость ограничена двумя концентрическими окружностями \( x^2+y^2=9; \quad x^2+y^2=16 \), т.е. представляет собой кольцо, а также говориться, что \( x=0, y=0; (x \geq 0, y \geq 0)\), получаем сегмент кольца в первой четверти см. рис.
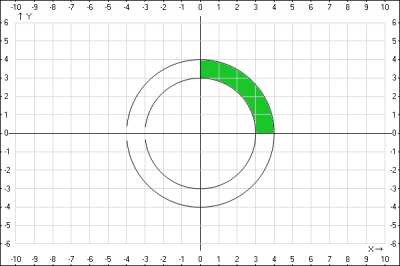
2. Найдем массу материальной пластины
используем формулу (1) $$ m = \int\int_D \frac{2x+5y}{x^2+y^2}dxdy = \quad (2)$$ т.к. плоскость D представляет собой сегмент кольца, для упрощения расчетов перейдем в полярную систему координат: \(x = \rho \cos(\phi); \quad y = \rho \sin(\phi); \quad dxdy = \rho d\rho d\phi \quad 0 \leq \phi \leq \frac{ \pi}{2}; \quad 3 \leq \rho \leq 4\), тогда$$\frac{2x+5y}{x^2+y^2} = \frac{2\rho \cos(\phi)+5\rho \sin(\phi)}{(\rho \cos(\phi))^2+(\rho \sin(\phi))^2} = $$$$ = \rho \frac{2 \cos(\phi)+5 \sin(\phi)}{\rho^2(\cos^2(\phi)+ \sin^2(\phi))} = \frac{2 \cos(\phi)+5 \sin(\phi)}{\rho}$$ подставляем результат в (2) $$m = \int\int_D \frac{2 \cos(\phi)+5 \sin(\phi)}{\rho} \rho d\rho d\phi = $$$$ = \int\int_D (2 \cos(\phi)+5 \sin(\phi)) d\rho d\phi =$$ подставляем границы интегрирования $$ = \int_0^{\frac{\pi}{2}}d\phi \int_3^4(2 \cos(\phi)+5 \sin(\phi)) d\rho = \quad (3) $$ найдем внутренний интеграл \( \int_3^4(2 \cos(\phi)+5 \sin(\phi)) d\rho = \) \( = (2 \cos(\phi)+5 \sin(\phi)) \int_3^4 d \rho = 2 \cos(\phi)+5 \sin(\phi)\) подставляем в (3) $$ = \int_0^{\frac{\pi}{2}}(2 \cos(\phi)+5 \sin(\phi)) d\phi = $$$$ = (2 \sin(\phi) - 5 \cos(\phi))|_0^{\frac{\pi}{2}} = (2+5) = 7$$
Ответ: масса материальной пластины равна \(m = 7\)

