Для решения данной задачи рассмотрим рисунок.

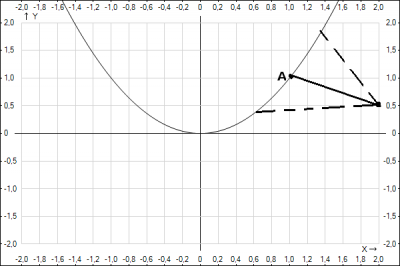
Нам нужно найти точку на параболе ближайшую $A$, т.е. расстояние между точкой на параболе и заданной точкой должно быть наименьшим. Поиск наименьшего расстояния сводится к поиску экстремумов функции. Исследуемой функцией будет расстояние между точками. Запишем формулу расстояния между точками

$$(x_2-x_1)^2+(y_2-y_1)^2 = \phi^2$$ где координаты $(x_1;y_1)$ и $(x_2;y_2)$ - точки, между которыми рассчитывается расстояние, $\phi$ - расстояние между точками. В нашем случае первая точка - заданная точка с координатами (2;0,5), вторая точка - точка на параболе с координатами (x;y). Учтем связь между координатами точек на параболе, т.е. $y = x^2$. Запишем уравнение расстояния между точками с учетом наших рассуждений, получим $$(x-2)^2+(x^2-\frac{1}{2})^2 = \phi^2 =>\phi = \sqrt{(x-2)^2+(x^2-\frac{1}{2})^2}$$ Получили функцию, зависящее от одной переменной $\phi(x)$, найдем экстремум (точку минимума), для этого найдем первую производную от расстояния и приравняем его к 0. $$\phi' = ( \sqrt{(x-2)^2+(x^2-\frac{1}{2})^2})' =0 =>$$ $$\frac{1}{2}\frac{2(x-2)+2(x^2-\frac{1}{2})^2*2x}{ \sqrt{(x-2)^2+(x^2-\frac{1}{2})^2}} =0 =>$$ Обратим внимание на то, что в числителе у нас стоит производная квадрата расстояния между точками, которую мы приравниваем к нулю (знаменатель $\ne$ 0 ), т.е. можно было сразу искать производную квадрата расстояния и приравнивать ее к 0, т.е. $((x-2)^2+(x^2-\frac{1}{2})^2)' =0$, также можно было открыть скобки и произвести упрощение, а затем находить производную, но производная понижает степень на 1, поэтому открывать скобки после нахождения производной, мне кажется проще, продолжаем $$2x-4+4x^3-2x =0 =>x=1$$ подставляем в уравнение параболы и находим $y = x^2 = 1$.

Ответ: ближайшая точка параболы к точке $(2;0,5)$ имеет координаты $(1;1)$.