Решение: Вычислим интеграл $$ \int\int_{V}\int(x^2+y^2)dxdydz$$ где область интегрирования V - (см. рис. 1) тело ограниченная поверхностью \(x^2+y^2=2z\) - параболоид вращения и \(z=2\) - плоскость параллельная плоскости xOy, проходящая через точку с координатами (0;0;2)
Нарисуем эту область
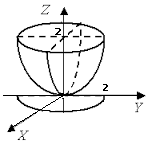
На рисунке видно, что тело, объем которого мы ищем имеет осевую симметрию, поэтому будем искать объем при \(x \geq 0; y \geq 0; z \geq 0\), полученный объем умножим на 4.
Для нахождения объема воспользуемся следующей формулой:
Если область интегрирования \(V\) определяется неравенства \(x_1 \leq x \leq x_2\), \(y_1(x) \leq y(x) \leq y_2(x)\), \(z_1(x,y) \leq z \leq z_2(x,y)\), где \(y_1(x), y_2(x), z_1(x,y), z_2(x,y)\) - непрерывные функции своих аргументов, то тройной интеграл вычисляется по формуле $$\int\int_{V}\int f(x,y,z)dxdydz = \int_{x_1}^{x_2}dx\int_{y_1(x)}^{y_2(x)}dy\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz$$ область \(V\) ограничена сверху плоскостью \(z = z_2(x,y)\), снизу - поверхностью \(z = z_1(x,y)\), а с боков - цилиндрической поверхностью с образующими, параллельными оси Oz, вырезающей на плоскости Oxy \(S_{xy}\), определенную неравенствами \(x_1 \leq x \leq x_2\), \(y_1(x) \leq y \leq y_2(x)\).
Обращаю внимание, что порядок интегрирования может быть любым.
Алгоритм вычисления тройного интеграла:
1. Расставим пределы интегрирования.
Рассмотрим проекцию тела на плоскость xOy. это будет круг радиусом 2, уравнение круга \(x^2+y^2=4 \). Круг с центром в начале координат, тогда в первой четверти \( 0 \leq x \leq 2 \), \(0 \leq y \leq \sqrt{4-x^2}\)
Рассмотрим переменную \(z\). Область снизу ограничена поверхностью \(x^2+y^2=2z => z = \frac{1}{2}(x^2+y^2)\), а сверху плоскостью \(z=2\).
2. Вычисляем тройной интеграл при известных границах $$\int\int_V\int(x^2+y^2)dxdydz = 4 \int_0^2dx\int_0^{\sqrt{4-x^2}}dy\int_{\frac{1}{2}(x^2+y^2)}^2(x^2+y^2)dz = \quad (2)$$ Упростим расчеты, т.к. область \(V\) имеет осевую симметрию и проектируется на плоскость xOy в круг
перейдем в цилиндрическую систему координат, применим формулу перехода
\( \int\int_V\int f(x;y;z)dxdydz = \int\int_V\int f(\rho \cos(x); \rho\sin(x))\rho d\rho d\phi dz \)
вводим замену \(x = \rho \cos(x); y = \rho\sin(x)\), тогда получим \(\sqrt{x^2+y^2} = \sqrt{(\rho \cos(x))^2+(\rho\sin(x))^2} = \sqrt{\rho^2} = \rho\) подставляем в интеграл $$ \int\int_V\int\sqrt{x^2+y^2}dxdydz = \int\int_V\int \rho *\rho d\rho d\phi dz = $$ теперь расставим пределы интегрирования (мы перешли в цилиндрическую систему координат) и найдем тройной интеграл \( 0 \leq \phi \leq \frac{\pi}{2}\), \( 0 \leq \rho \leq 2\), \(2z = x^2+y^2 => z = \frac{1}{2}\rho\), получаем $$= 4 \int_0^\frac{\pi}{2}d\phi \int_0^2 \rho^2 d\rho\int_{\frac{1}{2}\rho^2}^2 dz = 4 \frac{\pi}{2} \int_0^2 \rho^2 (2-\frac{1}{2}\rho^2) d\rho =$$$$ = 2 \pi \int_0^2 (2\rho^2 -\frac{1}{2}\rho^4) d\rho = 2 \pi (\frac{2}{3}\rho^3 -\frac{1}{2*5}\rho^5) |_0^2 =$$$$= 2 \pi (\frac{16}{3} -\frac{16}{5}) = \frac{64}{15}\pi$$
Ответ: объем равен \(V = \frac{64}{15}\pi\)

