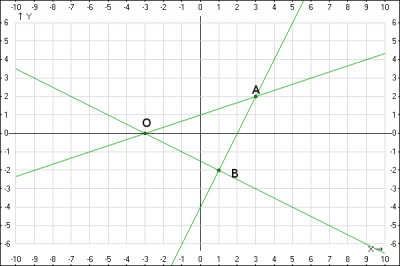
Решение: контур интегрирования состоит из трех отрезков, поэтому криволинейный интеграл по ломанной линии \(OAB\) - будем вычислять как сумму интегралов, взятых по каждому отрезку $$\oint_L = \int_{AO}+\int_{OB}+\int_{BA}$$
Алгоритм решения:
Положительным направлением обхода контура считается обход по контуру, при котором движение происходит против направления движения часовой стрелки.
1. Составим уравнения прямых AO, OB ,BA.
Т.к. известны координаты всех точек, применим уравнение прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \)
уравнение прямой AO \(\frac{x+3}{3+3} = \frac{y-0}{2-0} => y = \frac{1}{3}x+1\)
уравнение прямой BA \( \frac{x-3}{1-3} = \frac{y-2}{-2-2} => y = 2x-4\)
уравнение прямой OB \( \frac{x-1}{-3-1} = \frac{y+2}{0+2} => y = -\frac{1}{2}x- \frac{3}{2}\)
2. Используем уравнения прямых для преобразования криволинейного интеграла в определенный.
Применим формулу: если гладкая кривая AB задана явным уравнением \(y = f(x); \quad a \leq x \leq b\) и F = {P;Q} - вектор функция, определенная на этой кривой, то \(dy = y'(x)dx\) и $$ \int_{AB}P(x;y)dx+Q(x;y)dy = \int_a^b[P(x;y(x))+Q(x;y(x))y'(x)]dx $$
Прямая AO \(y = \frac{1}{3}x+1 => dy = \frac{1}{3}dx; \quad x_A=3; x_O=-3\) $$ \oint_Ly^2dx−x^2dy = \int_{OA} ( \frac{1}{3}x+1)^2 - x^2\frac{1}{3})dx = $$$$ = \int_{3}^{-3} ( \frac{1}{9}x^2+\frac{2}{3}x+1 - \frac{1}{3}x^2)dx = \frac{1}{9}\int_{3}^{-3} ( -2x^2+ 6x+9 )dx = $$$$ = \frac{1}{9} ( -\frac{2}{3}x^2+ 3x^2+9x )|_{3}^{-3} = -2$$
Прямая BA \(y = 2x-4 => dy = 2dx; \quad x_B=1; x_A= 3\) $$ \oint_Ly^2dx−x^2dy = \int_{AB}((2x-4)^2 - 2x^2)dx = $$$$ = \int_{1}^{3}((2x-4)^2 - 2x^2)dx = \int_{1}^{3}( 4x^2- 16x+16 -2x^2)dx = $$$$ = \frac{2}{3}x^3- 8x^2+16x |_{1}^{3} = -\frac{44}{3}$$
Прямая OB \(y = -\frac{1}{2}x- \frac{3}{2} => dy = -\frac{1}{2}dx; \quad x_O=-3; x_B= 1\) $$ \oint_Ly^2dx−x^2dy = \int_{BO}((-\frac{1}{2}x- \frac{3}{2})^2 + \frac{1}{2}x^2)dx = $$$$ = \int_{-3}^{1}((-\frac{1}{2}x- \frac{3}{2})^2 + \frac{1}{2}x^2)dx = \frac{1}{4} \int_{-3}^{1}((x+ 3)^2 + 2x^2)dx$$$$ = \frac{1}{4}(x^3 + 3x^2 + 9x) |_{-3}^{1} =10$$
3. Итоговый интеграл по замкнутому контуру \(OAB\) равен
$$ \oint_Ly^2dx−x^2dy = -2 - \frac{44}{3} + 10 = -\frac{20}{3}$$
Ответ: \( \oint_Ly^2dx−x^2dy = -\frac{20}{3}\)

