Решение:
а) найти вероятность \(p_1)\)
так как все события \(X \in \text{{-3,1,4,5}}\) образуют полную группу событий, то сумма вероятностей должна быть равна 1, т.е. \(p(X=-1) + p(X=1) + p(X=4) + p(X=5) =p_1 + 0.1 + 0.2 + 0.1 = 1 => p_1=0.6\). Заполняем таблицу: \begin{array}{|c|c|c|}\hline X& -3& 1& 4& 5\\ \hline \ p& 0.6& 0,1& 0,2& 0,1\\ \hline\end{array}
б) найти функцию распределения
Построим функцию распределения для случайной величины \(X\)
Для построения функции распределения дискретной случайной величины воспользуемся формулой $$F(x) = \sum_{x_k < x}P(X=X_k)$$
1. при \(x \leq -3 \) функция распределения
\(F(X) = \sum_{x_k < x}P(X=X_k) = 0\)
2. при \(-3 < x \leq 1 \) функция распределения
\(F(X) = \sum_{x_k < x}P(X=X_k) = P(X=-3) = 0 + 0.6 = 0.6\)
3. при \(1 < x \leq 4 \) функция распределения
\(F(X) = \sum_{x_k < x}P(X=X_k) = P(X=-3) + P(X=1) = 0 + 0.6+ 0.1 = 0.7\)
4. при \(4 < x \leq 5 \) функция распределения
\(F(X) = \sum_{x_k < x}P(X=X_k) = P(X=-3) + P(X=1) + P(X=4) = 0 + 0.6+ 0.1 + 0.2 = 0.9\)
5. при \( x > 5 \) функция распределения
\(F(X) = \sum_{x_k < x}P(X=X_k) = P(X=-3) + P(X=1) + P(X=4) + P(X=5) = 0 + 0.6+ 0.1 + 0.2 + 0.1 = 1\)
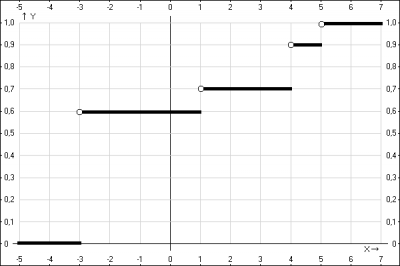
Получили функцию распределения $$F(X) = \begin{cases}0 & при & x \leq -3\\ 0.6 & при & -3 < x \leq 1 \\ 0.7 & при & 1 < x \leq 4 \\ 0.9 & при & 4 < x \leq 5 \\ 1 & при & x > 5 \end{cases} $$
График функции распределения
в) математическое ожидание, дисперсию, среднее квадратическое отклонение.
Найдем математическое ожидание
Математическое ожидание дискретной случайной величины рассчитывается по формуле
$$M(X) = x_1p_1 + x_2p_2 + ... + x_np_n = \sum_{k=1}^{n}x_kp_k$$
берем все данные из таблицы, получаем
$$M(X) = -3*0.6 + 1*0.1 + 4*0.2 + 5*0.1 = -0.4$$
Ответ: математическое ожидание \(M(X) = -0.4\)
Найдем дисперсия
Запишем закон распределения случайной величины \((X-M(X))^2\)
$$ \begin{array}{|c|c|c|}\hline X& (-3+0.4)^2& (1+0.4)^2 & (4+0.4)^2 & (5+0.4)^2 \\ \hline \\ p(X=i)& 0.6 & 0.1 & 0.2 & 0.1 \\ \hline \end{array} $$
Дисперсию дискретной случайной величины будем искать по формуле \(D(X) = \sum_{k=1}^{n}(X_k-M(X))^2p_k\)
$$D(X) = (-3+0.4)^2*0.6+(1+0.4)^2*0.1+(4+0.4)^2*0.2+(5+0.4)^2*0.1 = 11.04$$
Ответ: дисперсия равна \(D(X) = 11.04\)
Найдем среднеквадратическое отклонение
Среднеквадратическое отклонение находится по формуле \(\sigma(x) = \sqrt{D(x)}\)
подставляем в формулу дисперсию $$\sigma(x) = \sqrt{11.04} = 3.32 $$
Ответ: среднеквадратическое отклонение \(\sigma(x) = 3.32\)



