Решение: областью определения функции будет пересечение областей определения функций двух слагаемых
1. функция \(\frac{1}{\sqrt{y}}\) => \(D_f(y > 0 )\)
2. функция \(\ln(1-\frac{x^{2}}{9}+\frac{y^{2}}{16})\) => \(D_f(1-\frac{x^{2}}{9}+\frac{y^{2}}{16} > 0)\)
Составляем систему уравнений $$\begin{cases}y > 0\\1-\frac{x^{2}}{9}+\frac{y^{2}}{16} > 0\end{cases}=> \begin{cases}y > 0\\ \frac{x^{2}}{9}-\frac{y^{2}}{16} < 1\end{cases}$$
Область определения функции: \(D_f ={(x;y) \in R^2: \frac{x^2}{9}-\frac{y^2}{16} < 1 \text{ and } y > 0}\)
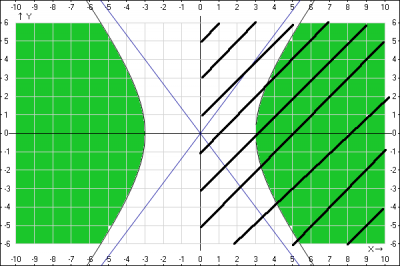
Графическое представление области определения:
1. строим область \( \frac{x^{2}}{9}-\frac{y^{2}}{16} < 1\) . Построим кривую \( \frac{x^{2}}{9}-\frac{y^{2}}{16} = 1\) - уравнение гиперболы, которая пересекает ось Ox в точках (-3;0), (3;0) и имеет две асимптоты, который находятся по формуле \(y = \pm \frac{b}{a}\), получаем \(y = \pm \frac{4}{3}\). Область, удовлетворяющая неравенству \( \frac{x^{2}}{9}-\frac{y^{2}}{16} < 1\) находится между кривых.
2. строим область \(y > 0\) - области, которая расположена справа от оси Oy
3. пересечение областей п.1,п.2 - искомая область определения функции.