Будем решать задачу по следующему плану.
1. Найдем касательную к графику функции \( y = x^2-2x+2 \) в точке с абсциссой \(x=2\)
2. Составим уравнение прямой, проходящей через две заданные точки \((0;2)\) и \((-3;0)\)
3. Найдем точку пересечения касательной и полученной прямой.
4. Построим чертеж.
Приступаем к решению
1. Найдем касательную к графику функции \( y = x^2-2x+2 \) в точке с абсциссой \(x=2\) для этого вспомним уравнение касательной в точке $$y=f(a)+f'(a)(x-a)$$где \(a\) - точка касания,
\(f(а)\) - значение функции в точке касания,
\(f'(a)\) - значение первой производной от функции \(f(x)\) в точке касания \(a\).
Найдем первую производную от функции \(f(x)\) $$f'(x) = (x^2-2x+2)' = 2x-2$$Найдем значение первой производной и значение функции в точке касания \(a=x=2\) $$f'(2) = 2x-2 = 2*2-2 =2$$$$f(2) = x^2-2x+2 = 2^2-2*2+2 =2$$Подставим полученные данные в уравнение касательной и получим его $$y=f(a)+f'(a)(x-a) => y = 2 + 2(x-2) =>$$$$ y = 2x-2$$
2. Составим уравнение прямой, проходящей через две заданные точки \((0;2)\) и \((-3;0)\) для этого воспользуемся формулой уравнения прямой линии, проходящей через две заданные точки $$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$$ подставим координаты точек $$\frac{y-2}{0-2}=\frac{x-0}{-3-0} =>-\frac{y-2}{2}=-\frac{x}{3} =>$$$$y=\frac{2}{3}x+2$$
3. Найдем точку пересечения касательной и прямой, для этого приравняем и уравнения $$2x-2 = \frac{2}{3}x+2 =>x=3$$подставим полученное значение у в одно из уравнения прямых и найдем \(y\)$$y = 2 + 2(x-2) =>y = 2+2(3-2) = 4$$Точка пересечения касательной и прямой имеет координаты \((3;4)\).
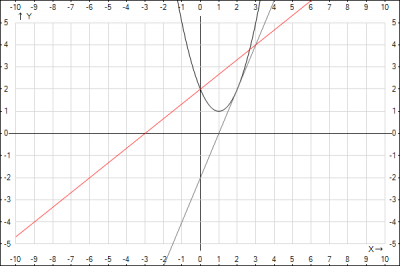
4. Построим чертеж, где
\(y = x^2-2x+2\) - парабола черного цвета
\(y = 2x-2\) - касательная к графику параболы серого цвета
\(y=\frac{2}{3}x+2\) - прямая, проходящая через две заданные точки красного цвета