В задании необходимо составить уравнение окружности. Запишем уравнение окружности $$(x-x_0)^2 + (y-y_0)^2 = R^2$$, где \((x_0;y_0)\) - координаты центра окружности, \(R\) - радиус окружности. Т.о. для составления уравнения окружности нам необходимо найти координаты центра окружности и радиус окружности. Приступим: в задании сказано, отрезок прямой содержащийся между осями координат - диаметр окружности. Найдем координаты этого отрезка (диаметра). Середина диаметра - центр окружности. Приступаем к нахождению центра окружности. Обозначим за \(A\) - точка пересечения с осью \(Ox\), а \(B\) - точка пересечения с осью \(Oy\), центр окружности обозначим \(O\). Как известно у точек пересечения с осью \(Oy\) \(x=0\) найдем эту точку \(5*0-4y+40 =0 =>y=10\). Получили координаты точки \(B\) пересечения с осью \(y\) \(B(0;10)\). Аналогично найдем координаты точки \(A\) - пересечение с осью \(Ox\). \(y=0 =>5x-4*0+40=0 =>x =-8\). Получили координаты точки пересечения с осью \(Ox\) \(A(-8;0)\). Найдем координаты центра окружности - середина отрезка \(AB\) для этого воспользуемся формулой координаты произвольной точки, которая делит отрезок в заданном отношении \(\lambda \), где $$ \lambda = \frac{AC}{CB} = \frac{R}{R}=1 $$$$ x= \frac{x_1+\lambda *x_2}{1+ \lambda} = \frac{x_1+x_2}{1+ 1} = \frac{x_1+x_2}{2}$$$$y= \frac{y_1+\lambda *y_2}{1+ \lambda} = \frac{y_1+y_2}{1+ 1} = \frac{y_1+y_2}{2}$$получили, что координаты середины отрезка равны полусумме соответствующих координат концов отрезка. Найдем координаты точки \(C\). $$x_с = \frac{x_A+x_B}{2} = \frac{-8 + 0}{2} = -4$$$$y_с = \frac{y_A+y_B}{2} = \frac{0 + 10}{2} =5$$Получили координаты центра окружности \(C(-4;5)\). Теперь осталось найти радиус окружности. Радиус будем искать как половина длины диаметра. Длина отрезка находится по формуле $$AB = \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} =\sqrt{(0+8)^2+(10-0)^2} = \sqrt{164}=2\sqrt{41}$$отсюда получим радиус окружности $$R= \frac{1}{2}AB = \sqrt{41} $$ Подставим полученные данные в уравнение окружности и получим искомое уравнение $$(x-x_0)^2 + (y-y_0)^2 = R^2 =>$$$$(x-(-4))^2 + (y-5)^2 = (\sqrt{41})^2 => $$$$(x+4)^2 + (y-5)^2 = 41$$Для проверки правильности составленного уравнения, построим его
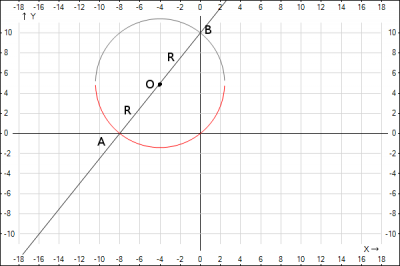
Ответ: уравнение окружности \( (x+4)^2 + (y-5)^2 = 41\)



