Данная задача на нахождение подобных треугольников и составление пропорции.
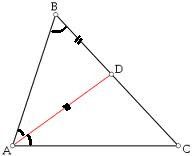
Рассмотрим рисунок. Т.к. \(AD\) - биссектриса угла \(A\), т.е. она разделила это угол на 2 равных, а это угол в 2 раза больше угла \(B\), то треугольник \(ΔABD\) - равнобедренный, а его боковые стороны равны \(BD=AD\). Теперь рассмотрим два треугольника \(ΔABC\) и \(ΔADC\) эти треугольники имеют один общий угол \(C\) и по равному углу \(B_{ΔABC}=A_{ΔADC}\), т.е. они подобны, признак подобия - по двум углам. Отмечу, что третий угол, соответственно \(D_{ΔADC}=A_{ΔABC}\). Составим пропорцию подобия $$\frac{AC_{ΔABC}}{DC_{ΔADC}}=\frac{BC_{ΔABC}}{AC_{ΔADC}} =>\frac{AC}{DC}=\frac{BD+DC}{AC}$$как мы помним \(BD=AD\), подставим все известные данные в формулу и получим $$\frac{9}{5}=\frac{AD+5}{9} => 5AD+25=81 => 4AD=56 => AD=11,2$$Ответ: биссектриса \(AD=11,2\)



