Решение:
Для нахождения площади фигуры, ограниченной заданными кривыми применим два метода.
1. Определенный интеграл и его геометрический смысл.
Вспомним геометрический смысл определенного интеграла: если функция \(f(x) \geq 0\) на отрезке \([a;b], a < b\), то определенный интеграл \(\int_a^bf(x)dx \quad\) равен площади криволинейной трапеции - фигуры, ограниченной линиями:
сверху \(y = f(x)\)
справа, слева \(x=a; x=b\)
снизу \(y=0\)
Согласно условия задачи, фигура ограниченная линиями \(y=x+1,y=0,x=2,x=3\), т.е. для нахождения площади фигуры применим определенный интеграл, применим формулу (1), получим $$S = \int_2^3(x+1)dx = $$ Для нахождения определенного интеграла, применим формулу Ньютона-Лейбница \(\int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a)\), получаем $$ = \frac{x^2}{2}+x |_2^3 = \frac{3^2}{3}+3 - \frac{2^2}{2} - 2 = \frac{5}{2} +1 = \frac{7}{2}$$
Ответ: площадь фигуры, ограниченной заданными кривыми, равна \(S = \frac{7}{2}\)
2. Площадь фигуры на декартовой системе координат.
Построим графики заданных функций на декартовой системе координат и найдем искомую фигуру.
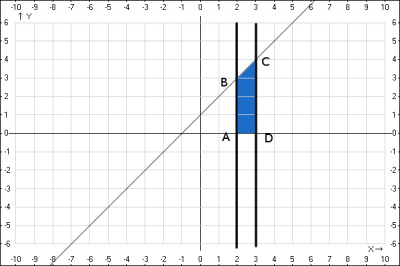
Из рисунка видно, что заданная фигура - прямоугольная трапеция ABCD.
Площадь трапеции находится по формуле \(S = \frac{a+b}{2}h\), где \(a;b\) - основания трапеции \(h\) - высота трапеции.
Найдем координаты вершин трапеции.
\(A(2;0) , \quad B(2;y(2)) => B(2;3) , \quad C(3;y(3)) => C(3;4), \quad D(3;0) \)
Найдем основания трапеции.
Основание \(AB = 3-0=3\)
Основание \(CD = 4-0=4\)
Высота трапеции \(AD = 3-2=1\)
Подставляем результат в формулу площади трапеции $$S = \frac{3+4}{2}*1 = \frac{7}{2}$$
Ответ: площадь фигуры, ограниченной заданными кривыми, равна \(S = \frac{7}{2}\)



