Найдите абсциссы точек пересечения графиков функций это значит найти значения \(x\) при которых графики функции пересекаются, т.е. в точке пересечения \(a\) значения функций равны \(f(a) =g(a)\). Найдем это значение \(x\) $$x^{\log_3x} = \frac{1}{27}x^4 =>x^{\log_3x} = (\frac{1}{3})^3x^4 =>$$прологарифмируем обе части уравнения $$\log_3{x^{\log_3x}} = \log_3{(\frac{1}{3})^3x^4} =>$$применяя формулу логарифма степени \(\log_ax^k=k\log_ax \) и формулу логарифма произведения \(\log_a(xy)=\log_ax+\log_ay \) получим $$\log_3x*\log_3x = \log_3{3}^{-3}+\log_3{x^4} =>\log_3^2x = -3+4\log_3{x} =>$$получили квадратное уравнение относительно \(\log_3x\) найдем его корни $$\log_3^2x -4\log_3{x}+3 =0 =>\log_3{x _{1,2}} = \frac{4 \pm \sqrt{16-4*3}}{2} = \frac{4 \pm 2}{2} =>$$$$\left[ \begin{gathered}\log_3{x} = 3\\\log_3{x} = 1\end{gathered}\right. =>\left[ \begin{gathered}\log_3{x} = 3\log_33\\\log_3{x} = \log_33\end{gathered}\right. =>$$$$\left[ \begin{gathered}\log_3{x} = \log_33^3\\\log_3{x} = \log_33\end{gathered}\right. =>\left[ \begin{gathered}x = 3^3=27\\x =3\end{gathered}\right.$$Получили значения абсциссы \(x\) точек пересечения графиков функции. Проверим наше решение графическим методом
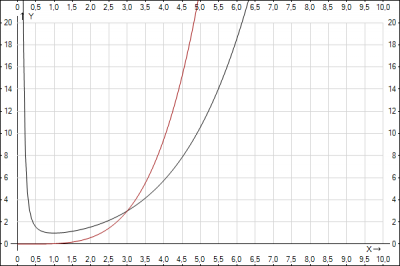
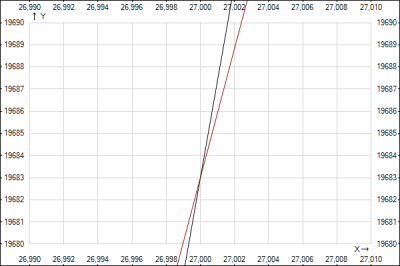
Ответ: абсциссы точек пересечения графиков функций \(x=3\), \(x=27\)



