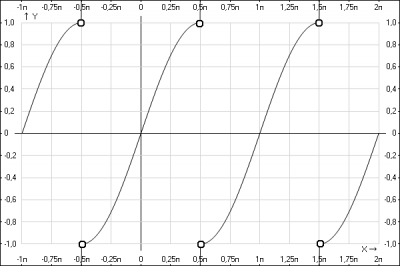
Решение: для построения графика функции нужно раскрыть модуль $$f(x)=tg(x)|\cos(x)|= \begin{cases} tg(x)\cos(x) & x \in (-\frac{\pi}{2}+2\pi n; \frac{\pi}{2}+2\pi n)\\tg(x)(-\cos(x)) & x \in (\frac{\pi}{2}+2\pi n; \frac{3}{2}\pi+2\pi n)\end{cases}=> $$$$f(x) = \begin{cases} \sin(x) & x \in (-\frac{\pi}{2}+2\pi n; \frac{\pi}{2}+2\pi n)\\-\sin(x) & x \in (\frac{\pi}{2}+2\pi n; \frac{3}{2}\pi+2\pi n)\end{cases}$$Область определения функции \(D_f: x \ne \frac{\pi}{2}+\pi n\). Рассмотрим график функции \(y = \sin(x)\) на интервале \((-\frac{\pi}{2};\frac{3}{2}\pi)\) - один период.
1. На интервале \((-\frac{\pi}{2};\frac{\pi}{2})\) строим график функции \(y = \sin(x)\)
2. На интервале \((\frac{\pi}{2};\frac{3}{2}\pi)\) строим график функции \(y = -\sin(x)\) - симметричное отражение графика функции \(y = \sin(x)\) относительно оси Ox.
График функции: