Для решения задачи необходимо вспомнить уравнение касательной к графику функции в заданной точке \(y = f(a) + f'(a)(x-a)\), где \(a\) - точка касания, \(f(a)\) - значение функции в точке касания, \(f'(a)\) - значение производной от функции \(f(x)\) в точке касания. Таким образом сформировался план решения задачи:
1. найти точки касания. По условию задачи - точки пересечения с осью \(Ox\).
2. найти угловой коэффициент касательной (первая производная функции \(f(x)\) в очке касания - \(f(a)\))
3. составить уравнение касательной к графику функции в точке касания и найти их точки пересечения
Приступаем.
Найдем точки касания - точки пересечения с осью \(Ox\). Как известно, в точках пересечения с осью значение функции \(f(a) = 0\). $$y=x^8+15x^4-16 = 0 =>$$ введем замену \(x^4 = t\), получили квадратное уравнение относительно \(t\) $$t^2+15t-16 = 0 =>t_{1,2}=\frac{-15 \pm \sqrt{225+4*16}}{2} = \frac{-15 \pm 17}{2} =>t_1 = 1, t_2 =-16$$т.к. \(t = x^4 \geq 0\), то остается только положительный корень \(x^4 = 1 => x = \pm 1\). Нашли два корня, т.е. две точки касания, в которые проведены касательные.
Найти угловые коэффициенты касательных в точках касания. Найдем первую производную и подставим в нее значение точек касания, т.е. полученных нами точек пересечения с осью \(Ox\). $$(x^8+15x^4-16)' = 8x^7 + 60x^3$$подставляем значения корней $$f'(1) = 8x^7 + 60x^3 = 8 + 60 = 68$$$$f'(-1) = 8x^7 + 60x^3 = -8 - 60 = -68$$
Составим уравнения касательных \(y = f(a) + f'(a)(x-a)\), т.к. точки касания - точки пересечения с осью \(Ox\), то значение \(f(a) = 0 \) для обеих касательных. Подставляем полученные данные в уравнение касательной и получаем
для точки \(x=1\) $$y = 68 (x-1) $$ для тоски \(x=-1\) $$y = -68 (x+1) $$найдем точку пересечения касательных. В точке пересечения прямых (касательных) значения \(y\) равны. Приравняем и получим $$68(x-1) = -68 (x+1) =>x-1 = -x-1 =>x=0$$Найдем значение функции \(f(0) =68(x-1)=-68 \). Получили точку пересечения двух прямых (касательных) \((0; -68)\)
Построим график функции \(y=x^8+15x^4-16 = 0 \) и касательных \(y = 68(x-1)\) - красная прямая \( y= -68 (x+1)\) - серая прямая
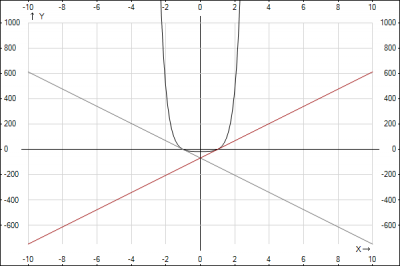
Ответ: точка пересечения двух касательных \((0;-68)\)



