Решение: для расчета площади фигуры построим графики функции и найдем граница искомой фигуры.
Уравнение \(x^2+y^2-2y=0\) это уравнение круга, приведем его к каноническому виду, применив метод выделения полного квадрата $$x^2+y^2-2y=0 => x^2+y^2-2y +1-1=0 => x^2+(y^2-1)^2=1$$ получили уравнение круга с центром в точке \((0;1)\) и радиусом \(r=1\)
Уравнение \(x^2+y^2-4y=0\) это уравнение круга, приведем его к каноническому виду, применив метод выделения полного квадрата $$x^2+y^2-4y=0 => x^2+y^2-2*2y +4-4=0 => x^2+(y^2-2)^2=4$$ получили уравнение круга с центром в точке \((0;2)\) и радиусом \(r=2\)
Уравнения \(y = \frac{x}{ \sqrt{3}}; \quad y = \sqrt{3}x\) - уравнения прямых, проходящих через начало координат.
Строим графики функций:
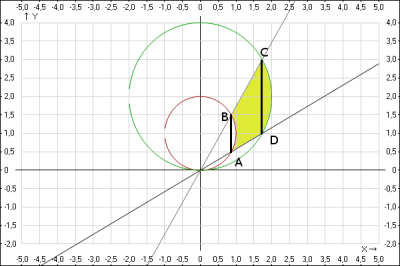
Искомая фигура закрашена, площадь которой будем искать (назовем ее область ABCD). Эту фигуру можно рассматривать как четырехугольник ABCD за вычетом сегмента малой окружности и добавлением сегмента большой окружности.
Для расчета площади нам нужны координаты точек пересечения прямых и окружностей
Найдем точки пересечения с малой окружностью (нас интересует координата x)
\(x^2+y^2-2y=0\) и прямая \(y = \frac{x}{ \sqrt{3}}\), подставляем уравнение прямой в уравнение круга $$x^2+(\frac{x}{ \sqrt{3}})^2-2\frac{x}{ \sqrt{3}}=0 => x^2+\frac{x^2}{3}-2\frac{x}{ \sqrt{3}}=0 => x =\frac{ \sqrt{3}}{2}$$
\(x^2+y^2-2y=0\) и прямая \(y = \sqrt{3}x \), подставляем уравнение прямой в уравнение круга $$x^2+(\sqrt{3}x)^2-2\sqrt{3}x = 0 => x^2+3x^2-2\sqrt{3}x=0 => x =\frac{ \sqrt{3}}{2}$$
Координаты \(x\) точек A и B одинаковые, это упрощает задачу
Найдем точки пересечения с большой окружностью (нас интересует координата x)
\(x^2+y^2-4y=0\) и прямая \(y = \frac{x}{ \sqrt{3}}\), подставляем уравнение прямой в уравнение круга $$x^2+(\frac{x}{ \sqrt{3}})^2-4\frac{x}{ \sqrt{3}}=0 => x^2+\frac{x^2}{3}-4\frac{x}{ \sqrt{3}}=0 => x = \sqrt{3}$$
\(x^2+y^2-2y=0\) и прямая \(y = \sqrt{3}x \), подставляем уравнение прямой в уравнение круга $$x^2+(\sqrt{3}x)^2-4\sqrt{3}x = 0 => x^2+3x^2-4\sqrt{3}x=0 => x = \sqrt{3}$$
Получили, что фигура ABCD - трапеция
Приступаем к поиску площади области ABCD
$$S_{обл_ABCD} = S_{трап_ABCD} - S_{сег.AB}+S_{сег.CD}$$
1. Найдем площадь трапеции, применим формулу площади фигуры, ограниченную двумя непрерывными кривыми \(y_1=g(x);y_2=f(x) => S=\int_a^b(f(x)-g(x))dx\)
$$S_{трап_ABCD} = \int_{\frac{\sqrt{3}}{2}}^{\sqrt{3}}(\sqrt{3}x - \frac{x}{\sqrt{3}})dx = $$ применяем формулу Ньютона-Лейбница \( \int_a^bf(x)dx = F(x)|_a^b = F(b) - F(a)\), получаем $$ = (\frac{\sqrt{3}}{2}x^2-\frac{1}{2\sqrt{3}}x^2)|_{\frac{\sqrt{3}}{2}}^{\sqrt{3}} = $$$$ =3\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}-\frac{3\sqrt{3}}{8}+\frac{\sqrt{3}}{8}=\frac{3\sqrt{3}}{4}$$
Площадь можно было найти по формуле площади трапеции \(S = \frac{a+b}{2}h\) , где a=AB=1, b=CD=2, \(h = x_Ax_D = \sqrt{3} - \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2}\), тогда площадь равна \(S_{трап_ABCD} = \frac{1+2}{2}\frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{4}\)
2. Находим площадь сегмента AB круга \( x^2+(y^2-1)^2= 1\)
\( x^2+(y^2-1)^2= 1 => y = \sqrt{1-x^2}+1\) $$S_{сег.AB} = \int_{\frac{\sqrt{3}}{2}}^1(\sqrt{1-x^2}+1)dx = \quad (1)$$ найдем интеграл \( \int \sqrt{1-x^2}dx = \) введем замену \( x = \sin(t) => dx = \cos(t)dt\), подставляем \( \int \sqrt{1- \sin^2(t)} \cos(t)dt = \int \cos(t) \cos(t)dt = \int \cos^2(t)dt = \) применим формулу косинуса двойного угла \( \cos^2(x) = \frac{\cos(2x)+1}{2}\), подставляем \(\int \frac{\cos(2x)+1}{2}dt = \frac{1}{2}t + \frac{1}{4}\sin(2t)\) применяем обратную замену \(x = \sin(t) => t = \arcsin(x)\) и учтем \( \sin(2t) = 2\sin(t)\cos(t) = 2\sin(t)\sqrt{1 - \sin^2(t)}\), получаем \( \frac{1}{2}\arcsin(x) + \frac{1}{2}x\sqrt{1-x^2} +C\), подставляем в (1) $$ = \frac{1}{2}\arcsin(x) + \frac{1}{2}x\sqrt{1-x^2} + x|_{\frac{\sqrt{3}}{2}}^1 = $$$$ =\frac{1}{2}\arcsin(1) + \frac{1}{2}1\sqrt{1-1^2} + 1 - ( \frac{1}{2}\arcsin(\frac{\sqrt{3}}{2}) + \frac{1}{2}\frac{\sqrt{3}}{2}\sqrt{1-(\frac{\sqrt{3}}{2}})^2 + \frac{\sqrt{3}}{2}) = $$$$ = 1 + \frac{\pi}{6}-\frac{5\sqrt{3}}{8}$$
3. Находим площадь сегмента CD круга \( x^2+(y^2-2)^2=4\)
\( x^2+(y^2-2)^2=4 => y = \sqrt{4-x^2}+2\) $$S_{сег.AB} = \int_{\sqrt{3}}^2(\sqrt{4-x^2}+2)dx = \quad (1)$$ $$ = \frac{4}{2}\arcsin(\frac{x}{2}) + \frac{1}{2}x\sqrt{4-x^2} + 2x|_{\sqrt{3}}^2 = $$$$ =2\arcsin(1) + \frac{1}{2}2\sqrt{4-2^2} + 2*2 - (2\arcsin(\frac{\sqrt{3}}{2}) + \frac{1}{2}\sqrt{3}\sqrt{4-(\sqrt{3})^2} + 2*\sqrt{3}) = $$$$ = 4-\frac{5 \sqrt{3}}{2}+\frac{\pi}{3}$$
4. Находим площадь области ABCD
$$S_{обл_ABCD} = S_{трап_ABCD} - S_{сег.AB}+S_{сег.CD} = \frac{3\sqrt{3}}{4} - ( 1 + \frac{\pi}{6}-\frac{5\sqrt{3}}{8}) + 4-\frac{5 \sqrt{3}}{2}+\frac{\pi}{3} =$$$$ = 3-\frac{9 \sqrt{3}}{8}+\frac{\pi}{6} \approx 1.58$$
Ответ: площадь фигуры (области ABCD) равна \(S \approx 1.58 \)



