В условии дана правильная треугольная пирамида, т.е. в основании лежит правильный треугольник (равносторонний), а боковые ребра пирамиды равны \(SA=SB=SC\). Высота пирамиды , опущенная на основание в точку \(O\) - центр правильного треугольника (точка равноудаленная от всех вершин треугольника). Центром правильного треугольника является точка пересечения его высот, медиан и биссектрис (эти точки совпадают в правильном треугольнике). Рассмотрим \(ΔSBC\) - равнобедренный треугольник, т.к. стороны \(SB=SC\), т.е. высота \(SH\) (апофема боковой грани пирамиды) опущенная на основание равнобедренного треугольника совпадает с ее медианой. Это нам нужно, чтобы определить, что точка \(H\) - середина стороны основания \(AC\), т.е. это точка - точка пересечения стороны \(AC\) и медианы (высоты, биссектрисы), опущенной из вершины \(B\) треугольника \(ΔABC\)
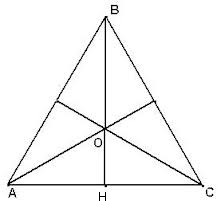
Из треугольника \(ΔSOH\) найдем высоту \(SO\). В треугольнике известна гипотенуза, а также можно найти катет \(OH\). Катет будем искать из \(ΔABC\) для этого воспользуемся свойством медиан - в точке пересечения медианы делятся в отношении \(\frac{BO}{OH}=\frac{2}{1}\), т.е. \(OH = \frac{1}{3}BH\). Из \(ΔBHC\) \(BH = BC*\sin 60 = 6*\frac{\sqrt 3}{2} = 3\sqrt 3\). Тогда \(OH = \frac{1}{3}BH = \frac{1}{3}*3 \sqrt 3 = \sqrt 3 \). Осталось по теореме Пифагора из \(ΔSBC\) найти высоту $$SO^2 = SH^2 - OH^2 => SO^2 = (2\sqrt 3)^2 - (\sqrt 3)^2 =>SO^2 = 12 - 3 = 9 => SO = 3$$Ответ: высота пирамиды равна \(SO=3\).





