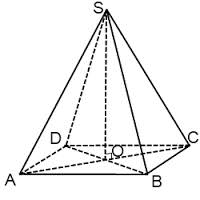
Правильная четырехугольная пирамида - пирамида в основании которой лежит правильный четырехугольник (квадрат), а боковые ребра равны \(SA=SB=SC=SD\). Рассмотрим треугольник \(ΔSAC\), по условию задачи - прямоугольный треугольник, о его катетах известно, что ни равны \(SA=SC\), т.е. он еще и равнобедренный. Приступаем к нахождению высоты пирамиды. Как известно, высота правильной четырехугольной пирамиды \(SO\) опущенная из вершины \(S\) на основание в точку \(O\) - центр квадрата, т.е. в точку пересечения диагоналей квадрата, а диагонали квадрата в точке пересечения делятся по полам. Теперь определился план решения задачи :
- находим диагональ квадрата. Диагональ \(AC\) найдем по теореме Пифагора \(AC=\sqrt{AB^2+BC^2} =\sqrt{2AB^2}=\sqrt{2*(\sqrt 2})^2 =2\). Нужно запомнить, что диагональ квадрата равна \(a \sqrt 2\), где \(a\) - сторона квадрата.
- из прямоугольного равнобедренного треугольника \(ΔSAC\), в котором уже известна гипотенуза найдем катет по теореме Пифагора \(SA^2+SC^2=AC^2 =>2SA^2 = 4 =>SA=\sqrt 2\)
- из треугольника \(ΔASO\) найдем \(SO\). Это прямоугольный треугольник. Гипотенуза известна \(SA =\sqrt 2\), катет \(AO = \frac{1}{2}AC=1\). Из теоремы Пифагора получаем $$SO^2 = SA^2 - AO^2 =>SO^2 = (\sqrt 2)^2 - 1^2 =>SO = 1$$
Ответ: высота правильной четырехугольной пирамиды равна \(SO = 1\).





