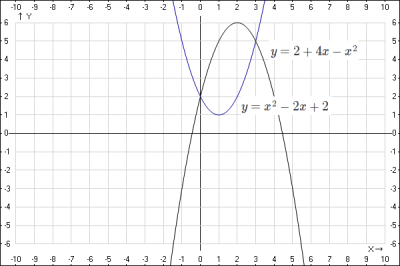
Решение: фигура в задании ограничена сверху параболой \(y = 2+4x-x^2\), а снизу \(y = x^2-2x+2\)
Площадь криволинейной фигуры ограниченной сверху графиком функции \(y_2 = f_2(x)\), снизу - графиком функции \(y_1 = f_1(x)\), слева и справки - прямыми \(x=a,x=b\), вычисляется по формуле $$S = \int_a^b(f_2(x) - f_1(x))dx \quad (1)$$
Найдем точки пересечения кривых, решим систему уравнений $$\begin{cases}y = 2+4x-x^2 \\y = x^2-2x+2\end{cases} => \begin{cases}2y = 4+2x \\y = x^2-2x+2\end{cases} => $$$$ \begin{cases}y = 2+x \\ 2+x = x^2-2x+2\end{cases} => \begin{cases}y = 2+x \\ x(x-3) = 0\end{cases} => $$$$ \begin{cases}y_1=2; \quad y_2=5 \\ x_1=0; \quad x_2=3\end{cases}$$
Подставляем уравнения кривых и координаты точек пересечения в формулу (1)
$$S = \int_0^3(2+4x-x^2 - x^2+2x-2)dx = \int_0^3(-2x^2+6x)dx = -\frac{2}{3}x^3+\frac{6}{2}x^2|_0^3 =$$$$ -\frac{2}{3}3^3+\frac{6}{2}3^2 = -18+27=9$$
Ответ: площадь фигуры, ограниченной заданными кривыми равна \(S = 9\)



