Решение: Контур интегрирования \(l\) состоит из трех отрезков, поэтому криволинейный интеграл по ломаной ABC будем вычислять как сумму интегралов, взятых по каждому из отрезков направление обхода - отрицательное, т.е. по часовой стрелке $$\oint_l =-( \oint_{AC} + \oint_{CB} + \oint_{BA}) \quad (1)$$
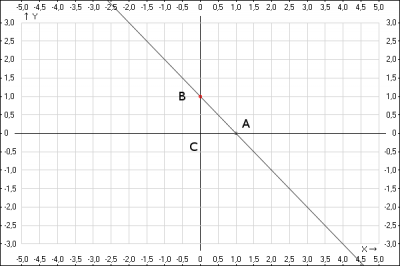
Найдем уравнение прямых старон:
AC: \(y = 0\)
CB: \(x = 0\)
BA: \(y = -x+1\)
С помощью полученных уравнений преобразуем криволинейный интеграл в определенный.
На прямой
AC: \(y = 0 => dy = 0 => \int_{AC} = \int_{l} xydx+2xy^2dy = 0\)
CB: \(x = 0 => dx = 0 => \int_{CB} = \int_{l} xydx+2xy^2dy = 0 \)
BA: \(y = -x+1 => dy = -dx, x_A=1; x_B=0 \) => \(\int_{BA} = \int_{l} xydx+2xy^2dy = \int_0^1 x(1-x)dx - 2x(1-x)^2dx = \int_0^1 (x-x^2 - 2x+4x^2-2x^3)dx \) =
\( \int_0^1(- x+3x^2-2x^3)dx = -\frac{1}{2}x^2+x^3-\frac{1}{2}x^4|_0^1 = -\frac{1}{2}+1-\frac{1}{2} = 0\)
Подставляем в (1)
$$\oint_l =-( \oint_{AC} + \oint_{CB} + \oint_{BA}) = -( 0 + 0 + 0) = 0$$
Ответ: \(0\)



