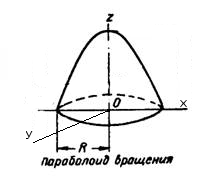
Решение: разрешим уравнение поверхности относительно переменной \(z\), получаем \(z = 1-\frac{x^2}{2} - \frac{y^2}{2}\). Получили уравнение параболоида вращения, вершина которого находится в точке \((0;0;1)\).
Часть параболоида вращения, которая отсекается горизонтальной плоскостью \(z=0\), проектируется на плоскость xOy в круг радиуса \(R\), найдем его
\(z = 0 \quad => \quad 0 = 1-\frac{x^2}{2} - \frac{y^2}{2} => x^2 + y^2 = 2 \) => \(R =\sqrt{2} \).
Для нахождения поверхностного интеграла первого рода применим формулу
$$ \iint_{S}F(x;y;z)dS = \iint_{S}F(x;y;z(x;y))\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}dxdy \quad (1)$$
Ищем частные производные функции поверхности \(z(x;y)\) $$\frac{\partial z}{\partial x} = (1-\frac{x^2}{2} - \frac{y^2}{2})'_x = -x$$$$\frac{\partial z}{\partial y} = (1-\frac{x^2}{2} - \frac{y^2}{2})'_y = -y$$
получили $$dS = \sqrt{1+x^2+y^2}dxdy$$ Сведем поверхностный интеграл к двойному по формуле (1)
$$ \iint_{S}(x^{2}+y^{2}+z-0.5)dS = \iint_{S}(x^{2}+y^{2}+1-\frac{x^2}{2} - \frac{y^2}{2}-0.5)\sqrt{1+x^2+y^2}dxdy = $$$$ = \frac{1}{2}\iint_{S}(x^2+y^2+1)\sqrt{1+x^2+y^2}dxdy = \frac{1}{2}\iint_{S}(x^2+y^2+1)^{\frac{3}{2}}dxdy \quad (2) $$Для дальнейшего нахождения двойного интеграла удобнее перейти к полярным координатам: \(\rho \in[0;\sqrt{2}]; \quad \phi \in [0;2\pi]\) , тогда \(x = \rho\cos(\phi), \quad y = \rho\sin(\phi)\), подставляем в (2) $$= \frac{1}{2}\int_{0}^{2\pi}\int_0^{\sqrt{2}}((\rho\cos(\phi))^2+(\rho\sin(\phi))^2+1)^{\frac{3}{2}}\rho d\rho d\phi = \frac{1}{2}\int_{0}^{2\pi}d\phi\int_0^{\sqrt{2}}(\rho^2+1)^{\frac{3}{2}}\rho d\rho = $$$$ = \frac{1}{2}2\pi \int_0^{\sqrt{2}}(\rho^2+1)^{\frac{3}{2}}\rho d\rho = \pi \int_0^{\sqrt{2}}(\rho^2+1)^{\frac{3}{2}}\rho d\rho =$$ введем замену \(\rho^2+1 = t^2 => 2\rho d\rho = 2tdt => \rho d\rho = tdt\), изменим границы \(\rho = 0 => t= \sqrt{\rho^2+1} = 1; \quad \rho = \sqrt{2} => t= \sqrt{\rho^2+1} = \sqrt{3}\) получаем $$ = \pi \int_1^{\sqrt{3}}(t^2)^{\frac{3}{2}}t dt = \pi \int_1^{\sqrt{3}}t^4 dt = $$$$ = \frac{\pi}{5}t^5|_1^{\sqrt{3}} = \frac{\pi}{5}3^\frac{5}{2} - \frac{\pi}{5} = \frac{\pi}{5}(9\sqrt{3} - 1)$$
Ответ: \(\frac{\pi}{5}(9\sqrt{3} - 1)\)



