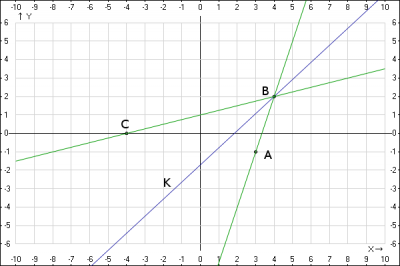
Задание: Дан треугольник АВС, А(3;-1), В(4;2), С(-4;0). Найти биссектрису ВК.
Решение: для нахождения уравнения биссектрисы воспользуемся формулой канонического уравнения прямой, которая проходит через заданную точку с координатами \((x_0;y_0)\), из условия задачи - точка В(4;2), параллельно направляющему вектору с координатами \(\vec{s}(m;n)\) $$\frac{x-x_0}{m} = \frac{y-y_0}{n} \quad (1)$$
Получили план решения задачи - нужно найти координаты направляющего вектора.
Известно, что сумму двух векторов \(\vec{a}+\vec{b} = \vec{c}\), выходящих из одной точки можно найти по правилу параллелограмма, результирующий вектор \(\vec{c}\) будет лежать на диагонали параллелограмма. Следствием из правила суммы будет следующее - если два вектора равны по модулю, то суммирующий вектор будет лежать на диагонали ромба. Применим свойства диагонали ромба - диагональ ромба лежит на биссектрисе угла. Т.о. нужно на сторонах треугольника из вершины \(B\) отложить два единичных вектора (орт) и найти их сумму.
1. Находим координаты орт на сторонах треугольника.
Найдем координаты векторов \(\vec{BA}\) и \(\vec{BC}\) по формуле \(X= x_i-x_j; Y=y_i-y_j \quad (2)\)
\(\vec{BA} = (3-4;-1-2) = (-1;-3)\)
\(\vec{BC} = (-4-4;0-2) = (-8;-2)\)
Находим модули этих векторов по формуле \(|\vec{a}| = \sqrt{x^2+y^2} \quad (3)\)
\(|\vec{BA}| = \sqrt{1+9} = \sqrt{10}\)
\(|\vec{BC}| = \sqrt{64+4} = \sqrt{68}\)
Находим координаты орт
\(\vec{a} = \frac{\vec{BA}}{|\vec{BA}|} = (-\frac{1}{\sqrt{10}};-\frac{3}{\sqrt{10}})\)
\(\vec{b} = \frac{\vec{BC}}{|\vec{BC}|} = (-\frac{8}{\sqrt{68}};-\frac{2}{\sqrt{68}})\)
2. Складываем единичные вектора (орты)
по формуле \( \vec{a}+ \vec{b} = (x_a+x_b;y_a+y_b)\), получаем
\( \vec{s} = \vec{a}+\vec{b} = (-\frac{1}{\sqrt{10}}-\frac{8}{ \sqrt{68}}; -\frac{3}{ \sqrt{10}} -\frac{2}{ \sqrt{68}})\)
3. Подставляем полученные координаты направляющего вектора \(\vec{s}\) и координаты точки B(4;2) в каноническое уравнение прямой (1)
$$\frac{x-4}{-\frac{1}{\sqrt{10}}-\frac{8}{\sqrt{68}}} = \frac{y-2}{-\frac{3}{\sqrt{10}} -\frac{2}{\sqrt{68}}} =>$$$$ y = \frac{4 \sqrt{10}-10 \sqrt{17}+ \sqrt{10}x+3 \sqrt{17} x}{4 \sqrt{10}+ \sqrt{17}}$$
Ответ: уравнение биссектрисы ВК \(y = \frac{4 \sqrt{10}-10 \sqrt{17}+ \sqrt{10}x+3 \sqrt{17} x}{4 \sqrt{10}+ \sqrt{17}} \)