Наибольшее и наименьшее значение функции на заданном множестве - экстремумы функции. Т.о. чтобы найти наибольшее значение функции необходимо найти его точку максимума (точку абсолютного (глобального) максимума). Ищем точку абсолютного максимума, т.к. в задании говорится о нахождении точки максимума на всем множестве области определения, а не на заданном отрезке. Поиск следующий.
- Находим производную $$y' =(\frac{5}{6x^2+2x+1})' =$$при меняем формулу производной дроби \((\frac{P(x)}{Q(x)})'=\frac{P'(x)Q(x)-Q'(x)P(x)}{Q^2(x)}\) получаем $$ =\frac{5'*(6x^2+2x+1)-5*(6x^2+2x+1)'}{(6x^2+2x+1)^2} = \frac{0-5*(12x+2)}{(6x^2+2x+1)^2}= -\frac{5*(12x+2)}{(6x^2+2x+1)^2}$$
- Как мы помним, первая производная дает нам ответ на вопрос о монотонности - функция монотонно возрастает (производная больше 0) или убывает (производная меньше 0). Отсюда и получим точку максимума, т.е. производная вначале возрастает ("+"), а при переходе через экстремум в точке \(x_0\) \(f'(x_0)=0\), далее убывает ("-"). Получили схему нахождения экстремума - находим точку в которой \(f'(x_0)=0\) и смотрим значения производной справа и слева от точки \(x_0\), если знак меняется с "+" на "-" - это и будет точка максимума (для справки, если на оборот с "-" на "+" - точка минимума).
Решаем
- Приравняем производную к нулю и найдем \(x_0\). $$ -\frac{5*(12x+2)}{(6x^2+2x+1)^2} = 0=>12x+2 =0 => x = -\frac{1}{6}$$
- смотрим значение производной слева от точки \(x_0=-\frac{1}{6}\) $$ f'(-1) =-\frac{5*(12 x+2)}{(6x^2+2x+1)^2} = -\frac{5*(12 *(-1)+2)}{(6(-1)^2+2(-1)+1)^2} >0 $$
- смотрим значение производной справа от точки \(x_0=-\frac{1}{6}\) $$ f'(0) =-\frac{5*(12 x+2)}{(6x^2+2x+1)^2} = -\frac{5*(12 *0)+2)}{(6*0^2+2*0+1)^2} < 0 $$
- анализируем изменение знака производной. Знак поменялся с "+" на "-".
Вывод это точка максимума
На рисунке изображен график функции \(y =\frac{5}{6x^2+2x+1}\), на нем видно, что наши рассуждения верны и в точке \(x_0=-\frac{1}{6}\) - функция принимает наибольшее значение, т.е. это точка абсолютного максимума (экстремум).
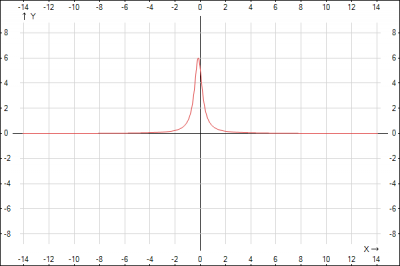
Ответ: наибольшее значение функции \(y =\frac{5}{6x^2+2x+1}\) будет в точке \(x_0=-\frac{1}{6}\)



