Решение: согласно условия, для искомой прямой известны точка и направление - угловой коэффициент прямой (искомая прямая перпендикулярная прямой в условии). Применим формулу уравнения прямой, проходящей через заданную точку в заданном направлении $$y - y_0 = k(x - x_0) \quad (1)$$ где \((x_0;y_0)\) - известная точка, принадлежащая прямой. Согласно условия задачи ее координаты M(-2;3).
Нужно найти угловой коэффициент. Для этого применим свойство угловых коэффициентов перпендикулярных прямых $$k_1*k_2=-1$$ Из условия известен угловой коэффициент одной их перпендикулярных прямых \(k=2\), тогда угловой коэффициент искомой прямой равен \(k=-\frac{1}{2}\). Подставляем угловой коэффициент и координаты точки в уравнение (1), получаем $$y - 3 = -\frac{1}{2}(x+2) =>$$$$y = -\frac{1}{2}x+2$$
Ответ: искомое уравнение прямой \(y = -\frac{1}{2}x+2\)
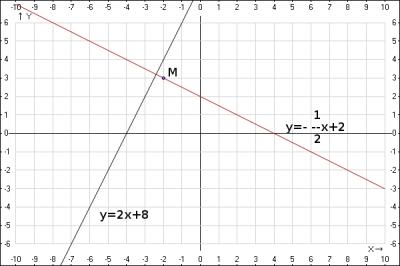
Для проверки построим рисунок