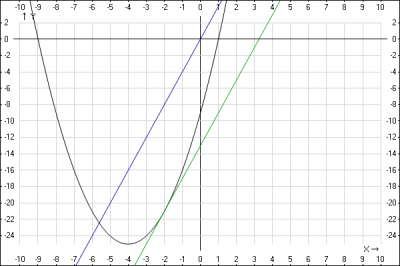
Задание: найти уравнение касательной к графику функции \(y = x^2+8x-9\), которая проходит параллельно прямой \(y=4x\).
Решение: уравнение касательной в точке равно $$y = f(x_0) + f'(x_0)(x-x_0) \quad (1)$$ В задании координаты точки нам не даны, но их можно найти из условия, что касательная параллельна заданной прямой. Согласно свойства угловых коэффициентов параллельных прямых \(k_1=k_2\). Угловой коэффициент прямой \(y = 4x\) равен \(k = 4\), угловой коэффициент касательной равен \(k_{кас} = f'(x_0)\) т.к \(k = k_{кас} = 4 =>\) получаем \(f'(x_0) = 4\). Найдем первую производную от функции $$(x^2+8x-9)' = 4 => 2x+8=4 => x=-2$$ получили \(x_0=-2\).
Найдем значение функции в точке \(x_0\), получаем \(f(x_0) = x_0^2+8x_0-9 = (-2)^2+8(-2)-9 = -21\)
Подставляем полученные значения в уравнение касательной (1) $$y = f(x_0) + f'(x_0)(x-x_0) => y = -21 + 4(x+2) = -21+4x+8 =>$$$$y = -13 + 4x$$
Ответ: уравнение касательной, параллельной заданной прямой \(y = -13 + 4x\)