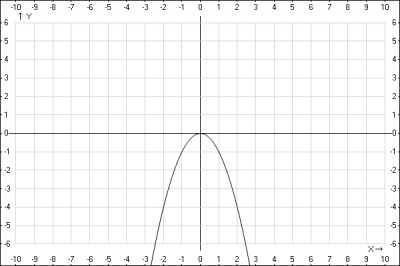
Решение: в задании нужно найти уравнение параболы, симметричной относительно оси Oy, которая проходит через начало координат. Каноническое уравнение параболы, симметричной относительно оси Oy, которая проходит через начало координат$$x^2 = 2py$$ Подставляем известную координаты и найдем параметр параболы \(p\). $$2^2 = 2p(-4) => p=-\frac{1}{2} $$ Получили уравнение параболы $$x^2 = -y => y = -x^2$$ получили параболу с параметром \(p=-\frac{1}{2} < 0\) - парабола направлена вниз.
Ответ: уравнение параболы \(y = -x^2\)