Тело брошено под углом к горизонту.
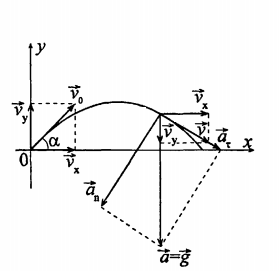
Перед тем как составить уравнения движения тела, определим тело поднимается вверх или уже падает. Найдем время, за которое тело поднимется до максимальной(верхней) точки своей траектории. Запишем уравнение вертикальной составляющей скорости $$v_y = v_0\sin\alpha - gt$$ В верхней точке траектории вертикальная скорость равна нулю \(v_y = 0\) $$ v_0\sin\alpha - gt = 0 => t = \frac{V_0\sin\alpha}{g} => t = \frac{14.7*\frac{1}{2}}{9,8}=0.75c$$ Получили, что тело движется, после прохождения верхней точки (обозначим \(t_2= t_1-t =1,25-0.75 =0.5c\)), т.е. падает.
Уравнения движения тела:
горизонтальная составляющая \(v_x = v_0\cos\alpha\)
вертикальная составляющая - тело движется равноускоренно с нулевой начальной скоростью \(v_y = gt\)
Полная скорость тела равна $$v = \sqrt{v_x^2+v_y^2}$$ По определению тангенциальное ускорение равно $$a_t = \frac{dv}{dt} = \frac{d(\sqrt{v_x^2+v_y^2})}{dt}$$$$a_t = (\sqrt{(v_0\cos\alpha)^2+(gt)^2})'_t = \frac{g^2t}{\sqrt{(v_0\cos\alpha)^2+(gt)^2}}$$ подставляем данные задачи $$a_t(0.5) = \frac{9.8^2*0.5}{\sqrt{(14.7*\frac{\sqrt{3}}{2})^2+(9.8*0.5)^2}} = 3.52\frac{m}{c^2}$$ Как известно ускорение \(a = \sqrt{a_t^2+a_n^2}\). Ускорение с которым движется тело равно \(a=q\) => $$a_n = \sqrt{a^2-a_t^2} = \sqrt{g^2-a_t^2}$$ подставляем данные $$a_n =\sqrt{9.8^2-5.32^2} = 9.15\frac{m}{c^2}$$
Ответ: нормальное ускорение равно \(a_n = 9.15\frac{m}{c^2}\), тангенциальное ускорение равно \(a_t = 3.52\frac{m}{c^2}\)



