Решение:
Введем обозначение: \(q = 0.4\) - вероятность отказа прибора, \(p = 0,6 \) - вероятность работоспособности каждого прибора.
Для того, чтобы ответить на вопрос о вероятности прохождения сигнала через систему, будем систему на крупные блоки, затем делить блоки на более мелкие и так до прибора.
1. Рассмотрим систему, состоящую из двух блоков. Параллельное соединение блоков.
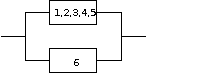
первый блок - приборы\(1,2,3,4,5\), вероятность прохождения сигнала через этот брок равна \(p_{1,2,3,4,5}\), а вероятность не прохождения \(q_{1,2,3,4,5}\)
второй блок - приборы\(6\), вероятность прохождения сигнала через этот брок равна \(p_{6}\), а вероятность не прохождения \(q_{6}\), согласно условия задачи \(p_{6} = 0,6;q_{6} = 0.4\)
Блоки соединены параллельно. Сигнал пройдет через эти блоки, если будет исправен хотя бы один блок (один из блоков или оба блока).
Найдем все вероятности
\((1;1)\) оба блока исправны. Вероятность будем искать по формуле произведения \(P(1;1) = p_{1,2,3,4,5}p_{6}\)
\((1;0)\) блок \({1,2,3,4,5}\) - исправен, а блок \({6}\) - нет. Вероятность равна \(P(1;0) = p_{1,2,3,4,5}q_{6}\)
\((0;1)\) блок \({1,2,3,4,5}\) - неисправен, а блок \({6}\) - исправен. Вероятность равна \(P(0;1) = q_{1,2,3,4,5}p_{6}\)
\((0;0)\) блок \({1,2,3,4,5}\) - неисправен, а блок \({6}\) - неисправен. Вероятность равна \(P(0;0) = q_{1,2,3,4,5}q_{6}\)
Вероятность прохождения сигнала будет равна $$P_{сист.} = P(1;1)+P(1;0)+P(0;1) = 1 - P(0;0) = 1 - q_{1,2,3,4,5}q_{6} \quad (1)$$
2. Найдем вероятность \(q_{1,2,3,4,5}\). Последовательное соединение блоков.
Рассмотрим блок, состоящий из приборов \({1,2,3,4,5}\) . Представим этот блок в следующем виде
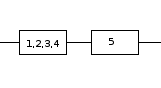
последовательное соединение блоков
Сигнал пройдет через устройства только при условии работоспособности одновременно двух блоков \(p_{1,2,3,4,5} = p_{1,2,3,4}p_{5} => q_{1,2,3,4,5} = 1-p_{1,2,3,4}p_{5}\) Получили формулу для расчета вероятности работоспособности блока при последовательном соединении блоков. Подставляем в (1) $$P_{сист.} = 1 - q_{1,2,3,4,5}q_{6} = 1 - (1-p_{1,2,3,4}p_{5})q_{6} \quad (2)$$
3. Найдем вероятность \(p_{1,2,3,4}\). Параллельное соединение блоков.
Рассмотрим блок, состоящий из приборов \({1,2,3,4}\), он состоит из блоков \({1,2}\) и \({3,4}\) - соединены параллельно.
В п.1 мы получили формулу вероятности для параллельного соединения блоков \(p_{1,2,3,4} = 1 - q_{1,2}q_{3,4}\) подставляем в (2) $$P_{сист.} = 1 - (1-p_{1,2,3,4}p_{5})q_{6} = 1 - (1-(1 - q_{1,2}q_{3,4})p_{5})q_{6} \quad (3)$$
4. Найдем вероятности \(q_{1,2}\), \(q_{3,4}\). Последовательное соединение приборов.
Рассмотрим блоки \({1,2}\), \({3,4}\) элементы которых соединены последовательно $$p_{1,2} = p_{1}p_{2} => q_{1,2} = 1 - p_{1}p_{2}$$$$p_{3,4} = p_{3}p_{4} => q_{3,4} = 1 - p_{3}p_{4}$$ Подставляем в (3) $$P_{сист.} = 1 - (1-(1 - (1 - p_{1}p_{2})(1 - p_{3}p_{4}))p_{5})q_{6} \quad (4)$$ Согласно условия задачи \(p = p_{1}=p_{2}= ... =p_{6} = 0,6\), \(q = q_{1}=q_{2}= ... =q_{6} = 0,4\), получаем $$P_{сист.} = 1 - (1-(1 - (1 - p^2)^2)p)q = 1 - (1-(1 - (1 - (0.6)^2)^2)0.6)0.4 \approx 0.7417$$
Ответ: вероятность того, что сигнал пройдет систему равна \(P_{сист.} \approx 0.7417\)



