В правой и левой части неравенства логарифмы с одним основанием, при этом основание меньше 1, т.е. это убывающая функция, а это означает, что большему значению \(x\), соответствует меньшее значение функции. На основании указанной монотонности перейдем к рассмотрению аргументов (выражение под логарифмом) при этом знак неравенства поменяем на противоположный $$\log_{\frac{1}{\pi}}(2x^2-5x) \geq \log_{\frac{1}{\pi}}(2x-3) =>2x^2-5x \leq 2x-3 =>2x^2-7x + 3 \leq 0$$ Найдем корни уравнения второго порядка $$2x^2-7x + 3 = 0 =>x_{1,2}=\frac{7 \pm \sqrt{49-4*3*2}}{2*2}=\frac{7 \pm 5}{4} => x_1=3, x_2=\frac{1}{2}$$зная корни уравнения, вернемся к неравенству, разложив многочлен на множители $$2x^2-7x + 3 \leq 0 =>(x-3)(x-\frac{1}{2})\leq 0$$методом змейки находим интервалы при которых значение \(x\) удовлетворяет неравенству получили, что \(x \in [0;3]\) (змейка черного цвета). Учтем ОДЗ логарифма $$\begin{cases}2x^2-5x >0\\ 2x-3> 0\end{cases} =>\begin{cases}x(x-\frac{5}{2}) >0\\ x>\frac{3}{2} \end{cases}$$(змейка красного цвета и голубого) ОДЗ \(x \in (\frac{5}{2}; +\infty)\). Найдем пересечение, полученного решения и ОДЗ.
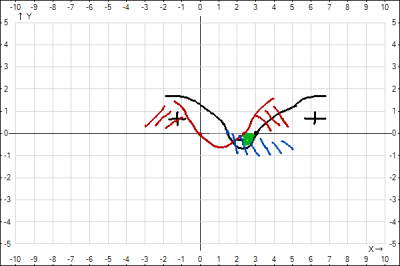
Ответ: \(x \in (\frac{5}{2};3]\)



