Дано координати вершин трикутника АВС.
Знайти:
1) координати точки перетину медіан трикутника;
2) косинус внутрішнього кута А.
A(4;4;-2),B(11;-2;-2),C(0;-6;2).
Розв'язання:
Знайдемо координати векторів \( \vec{AB}; \vec{AC};\vec{BC}\)
Координати вектора знаходимо за формулами: $$X = x_2-x_1;\quad Y = y_2-y_1; \quad Z = z_2-z_1 \quad (1)$$
У даному випадку: $$\vec{AB} = (11-4;-2-4;-2+2) = (7;-6;0)$$$$ \vec{AC} = (0-4;-6-4;2+2) = (-4;-10;4)$$$$\vec{BC} = (0-11;-6+2;2+2) = (-11;-4;4)$$
1) координати точки перетину медіан трикутника;
Знайдемо координати точки перетину медіан.
Розглянемо малюнок.
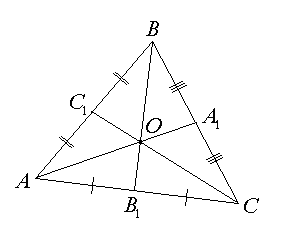
Вектор \(\vec {AA_1} \) лежить на медіані трикутника. Як відомо в точці перетину медіани діляться у відношенні \(2: 1 \), тобто вектор \( \vec {AO} = \frac{2}{3} \vec{AA_1} \)
Знайдемо координати цього вектора і за формулою (1) знайдемо координати шуканої точки \(O \).
З малюнка видно, що $$ \vec{AA_1} = \vec{AB} + \frac{1}{2} \vec{BC} => $$$$ \vec{AO} = \frac{2}{3} \vec{AA_1} = \frac{2}{3} (\vec{AB} + \frac{1}{2} \vec{BC}) => $$$$ \vec{AO} = \frac{2}{3} \vec{AB} + \frac{1}{3} \vec{BC} \quad (2) $$
Знайдемо координати векторів
\(\frac{2}{3} \vec{AB} = (7 \frac{2}{3}; - 6 \frac{2}{3}; 0 \frac{2}{3}) = ( \frac{14}{3}; - 4; 0) \)
\( \frac{1}{3} \vec{BC} = (-11 \frac{1}{3}; -4 \frac{1}{3}; 4 \frac{1}{3}) = (- \frac{11}{3}; - \frac{4}{3}; \frac{4}{3}) \)
Підставляємо результат в (2) $$ \vec{AO} = ( \frac{14}{3} - \frac{11}{3}; - 4 \frac{4}{3}; 0 + \frac{4}{3}) = (1; - \frac{16}{3}; \frac{4}{3}) $$
З формули (1) отримуємо шукані координати точки \(O \), де \((x_1; _1; z_1) \) - координати точки \(A (4; 4; -2) \)
\(x_o = X+x_1 = 1+4 =5\)
\(y_o = Y+y_1 = -\frac{16}{3}+4 = -\frac{4}{3}\)
\(z_o = Z+z_1 = \frac{4}{3}-2 = -\frac{2}{3}\)
Відповідь: координати точки перетину медіан трикутника \(O(5;-\frac{4}{3};-\frac{2}{3})\)
2) косинус внутрішнього кута \( \angle A\):
Будемо шукати кут \( \angle A \) як кут між векторами \( \vec{AB}; \vec{AC}\).
Кут між векторами знайдемо за допомогою формули: $$ \cos(a) = \frac{X_1X_2+Y_1Y_2+Z_1Z_2}{ \sqrt{X_1^2+Y_1^2+Z_1^2} \sqrt{X_2^2+Y_2^2+Z_2^2}}$$ Підставляємо координати векторів $$ \cos( \angle A) = \frac{7(-4)+(-6)(-10)+0*4}{ \sqrt{7^2+(-6)^2+0^2} \sqrt{(-4)^2+(-10)^2+4^2}} => $$$$ \cos( \angle A) = \frac{16}{ \sqrt{2805}} \approx 0.302$$
Відповідь: косинус внутрішнього кута \( \cos( \angle A) \approx 0.302 \)



