Общее уравнение линии второго порядка можно представить в виде: $$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$$ приведем уравнение второго порядка к более простому виду, т.е. каноническому виду
- Проверяем наличие в уравнении члена \(Bxy\), т.к. \(Bxy=0\), поворот системы координат делать не нужно приступаем к следующему этапу решения.
- В уравнении есть квадраты обоих неизвестных. Преобразуем левую часть заданного уравнения путем выделения полного квадрата: $$x^2 + y^2 – 4x +6y + 4 = 0 => x^2 – 2*2x+4-4+ y^2 +2*3y+9-9 + 4 = 0$$$$ (x – 2)^2+ (y +3)^2-9 = 0 =>(x – 2)^2+ (y +3)^2 = 3^2$$
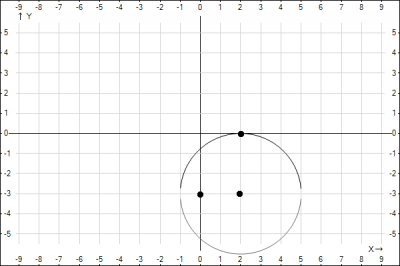
Получили уравнение окружности с центром в точке \((2;-3)\) и радиусом \(R=3\)
Построим данную кривую