Решение:
Находим функцию распределения, для этого рассмотрим три интервала, заданные для плотности распределения
1. интервал \( x < -\frac{a}{2}\), плотность распределения на этом интервале равна f(x) =0.
Интеграл от функции плотности распределения f(x) на промежутке \((-\infty;x)\) - равен значению функции распределения F(x) для верхнего предела интегрирования, т.е \(F(x) = \int_{-\infty}^{x}f(t)dt \). Находим интеграл на этом интервале при f(x)=0 $$F(x) = \int_{-\infty}^{x}0dt = 0$$ Получили, что на интервале \((-\infty;-\frac{a}{2})\) функция распределения равна F(x) = 0.
2. интервал \( -\frac{a}{2} < x < \frac{a}{2}\), плотность распределения на этом интервале равна \(f(x) =\frac{1}{a}\). По схеме предыдущего пункта находим $$F(x) = \int_{-\infty}^x\frac{a}{2}dt = \int_{-\infty}^{-\frac{a}{2}}0dt + \int_{-\frac{a}{2}}^{x} \frac{1}{a}dt = $$$$ = 0 + \frac{1}{a}t|_{-\frac{a}{2}}^x = \frac{1}{a}x + \frac{1}{2}$$ Получили, что на интервале \((-\frac{a}{2}; \frac{a}{2})\) функция распределения равна \(F(x) = \frac{1}{a}x + \frac{1}{2}\).
3. интервал \( \frac{a}{2} < x \), плотность распределения на этом интервале равна \(f(x) = 0\). По схеме предыдущего пункта находим $$F(x) = \int_{-\infty}^x\frac{1}{a}dt = \int_{-\infty}^{-\frac{a}{2}}0dt + \int_{-\frac{a}{2}}^{\frac{a}{2}} \frac{1}{a}dt + \int_{\frac{a}{2}}^{x}0dt = $$$$ =0+ \frac{1}{a}t|_{-\frac{a}{2}}^{\frac{a}{2}} + 0 = \frac{1}{a}*\frac{a}{2} + \frac{1}{a}*\frac{a}{2} = \frac{1}{2} + \frac{1}{2} = 1$$
Получили, что на интервале \((\frac{a}{2}; \infty)\) функция распределения равна \(F(x) = 1\).
4. График функции распределения.
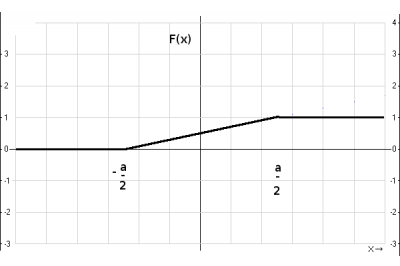
Ответ: интегральная функция распределения имеет вид $$F(x) = \begin{cases}0 & x < -\frac{a}{2} \\ \frac{1}{a}x + \frac{1}{2} & -\frac{a}{2} < x < \frac{a}{2} \\ 1 & \frac{a}{2} < x \end{cases} $$



