Решение: распределение симпсона - треугольное распределение см.рис.
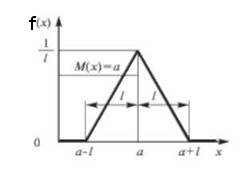
В задании говорится, что генерируется 100 чисел, но ничего не говорится о диаппазоне - \((a-l;b+l)\). В тоже время известно, что математическое ожидание равно \(M(x) = 0\), т.е. \(M(x) = \frac{a-l+a+l}{2} = 0 => a=0 \). Получили параметры закона, т.е. интервал, в котором изменяется случайная величина X - \((-l;l)\), где \(l\) - отклонение.
Плотность распределения Симпсона примет вид см. рис.
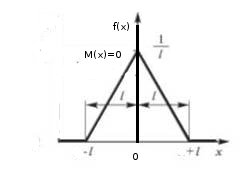
$$f(x) = \begin{cases} 0, & x < -l \\ \frac{x+l}{l^2} & -l \leq x < 0 \\ \frac{l-x}{l^2} & 0 \leq x < l \\ 1 & x \geq l \end{cases}$$ Согласно условия задачи \(P(x > 5) = 0,3\) Вероятность непрерывной случайной величины X на интервале (a;b) равна $$P(a < X < b) = \int_a^bf(x)dx$$ т.е. у нас известен интеграл $$P(5 < X < l) = \int_5^l \frac{l-x}{l^2}dx = 0,3 => \int_5^l (\frac{1}{l} -\frac{x}{l^2})dx = 0,3 =>$$$$ \frac{1}{l}x -\frac{x^2}{2l^2}|_5^l = 0,3 => 1 - \frac{1}{2} -\frac{5}{l} +\frac{25}{2l^2} = 0,3 =>$$ решаем квадратное уравнение относительно неизвестной \(l\)$$0,2 -\frac{5}{l} +\frac{25}{2l^2} = 0 => 0,4l^2 -10l + 25 = 0 => $$$$2l^2 -50l + 125 = 0 => l = \frac{5}{2}(5 \pm \sqrt{15}) $$ Получили два возможных решения.
Аналогичный ответ можно было получить просто найдя неизвестную \(l\) из площади закрашенного треугольника:
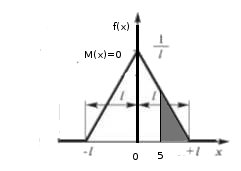
прямоугольный треугольник с катетами \(a = l-5; b=f(5) = \frac{l-5}{l^2}\), подставляем в формулу площади $$S = \frac{1}{2}ab = \frac{1}{2}(l-5)\frac{l-5}{l^2} = 0,3 => $$$$ l^2-10l+25 = 0,6l^2 => 0,4l^2-10l+25 = 0$$ Получаем аналогичный ответ.
Ответ: отклонение \(l = \frac{5}{2}(5 \pm \sqrt{15})\)



