Решение: согласно условия задачи:
1. известно, что фокусы эллипса лежат на оси Ox, симметрично начало координат, т.е. центр эллипса это точка \(O(0;0)\), а уравнение эллипса будет иметь вид $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (2)$$ Т.к. фокусы лежат на оси Ox, из этого следует связь между полуосями \(a > b\) Для того, чтобы получить уравнение эллипса, нужно найти полуоси \(a;b\).
2. известно , что расстояние между фокусами \(2c = 6 => c = 3\).
В п.1 было показано, что полуоси \(a;b\) связаны неравенством \(a > b \) и тогда выполняется следующее соотношение $$a^2 = c^2 + b^2 => a^2 = 3^2 + b^2 \quad (2)$$
3. известно, что расстояние между директрисами равно \(\frac{16*2}{3}\).
Уравнение директрисы в общем виде \(x = \pi \frac{a^2}{c}\), согласно условия задачи \(2x = \frac{16*2}{3} => x = \frac{16}{3} => \frac{a^2}{c} = \frac{16}{3} => \), известно, что \(c = 3\), получим \(\frac{a^2}{3} = \frac{16}{3} => a = 4\)
Полученное значение полуоси, подставляем в (2) $$a^2 = 3^2 + b^2 => 4^2 = 3^2 + b^2 => b^2 = 7$$
Подставляем значения полуосей \(a^2=16;b^2=7\) в каноническое уравнение эллипса, получаем искомое уравнение $$\frac{x^2}{16} + \frac{y^2}{7} = 1$$
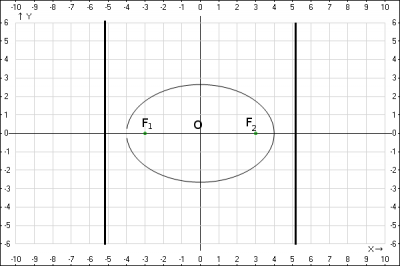
Строим рисунок: