Рассмотрим рисунок
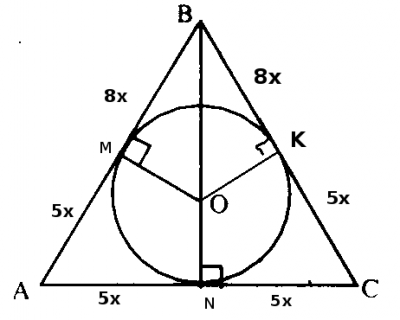
На основании свойства окружности вписанной в угол можно сделать вывод, что \(MB=BK; CK=CN; AN=AM\). Обозначим длину стороны \(BC = 8x+5x = 13x\). Известно, что периметр треугольника равен 72. Подставим, полученные значения в периметр и найдем длины сторон \(P_{ABC}=8x+8x+5x+5x+5x+5x=36x = 72 =>x=2 \).Длины сторон равны \(AB =BC = 26\), \(AC = 20\). Площадь треугольника можно найти по формуле \(S_{ABC} =\sqrt{p*(p-a)(p-b)(p-c)}\), где \(p=\frac{26+26+20}{2} =36\). $$S_{ABC} =\sqrt{p*(p-a)(p-b)(p-c)}=$$$$=\sqrt{36*(36-26)(36-26)(36-20)}=\sqrt{36*10*10*16}=6*10*4=240$$Ответ площадь \(S_{ABC} = 240\)





