Рассмотрим рисунок
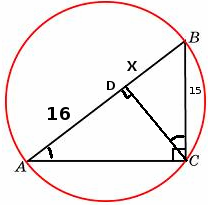
Обозначим за \(BD=x\). Рассмотрим \(ΔABC\) и \(ΔDBC\) они подобны по двум углам (Это прямоугольные треугольники и у них один угол общий). Составим пропорцию подобия $$\frac{BC}{AB}=\frac{DB}{BC} => \frac{15}{16+x}=\frac{x}{15}=>$$$$15^2=x(16+x)=>x^2+16x-15^2=0$$решаем квадратное уравнение $$x_{1,2}=\frac{-16 \pm \sqrt{16^2+4*15^2}}{2}=\frac{-16 \pm 34}{2}$$ т.к. длина отрезка может быть только положительной, получаем \(DB=x=9\). Как известно гипотенуза описанного прямоугольного треугольника это и есть диаметр описанной окружности, получаем \(D = AD+DB = 16+9 =25\). Ответ диаметр окружности равен \(D=25cm\).





