Решение: каноническое уравнение параболы, симметричной относительно оси Ox с вершиной в начале координат \(y^2 = 2px\). Найдем параметры параболы \(p\), подставим координаты известной точки \(A(2;-10)\), получаем \(10^2 = 2p*2 => p=25\), т.о. получили
1. уравнение параболы $$y^2 = 50x$$
2. найти фокус параболы.
Координаты фокуса параболы \(F(\frac{p}{2};0)\) , подставляем значение найденного параметра параболы, получаем координаты фокуса параметра \(F(12,5;0)\)
3. найти директрису параболы.
Уравнение директрисы параболы имеет вид \(x = -\frac{p}{2}\) => получаем $$x = -\frac{25}{2} => x = -12,5$$
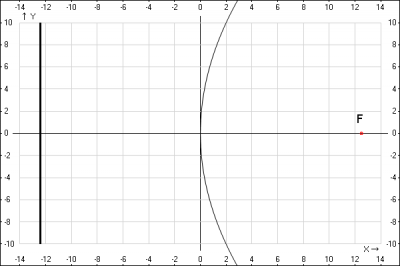
4. построим параболу: