Рассмотрим рисунок
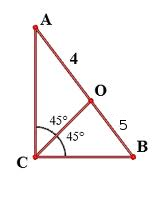
Вспомним свойство биссектрисы треугольника : биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам $$\frac{AO}{OB}=\frac{ AC}{CB}$$подставим в формулу значения и получим \(\frac{ AC}{CB} = \frac{4}{5} => AC = \frac{4}{5}CB\) эта формула дала нам связь между катетами, найдем их, а зная катеты найдем площадь прямоугольного треугольника. Катеты найдем по формуле Пифагора $$ AC^2+CB^2 = AB^2 => \frac{16}{25}CB^2+CB^2=9^2 =>CB = \sqrt{9^2*\frac{25}{41}}=45*\frac{1}{\sqrt{41}}$$Зная один из катетов и их соотношение найдем площадь $$S_{ABC} = \frac{1}{2}* AC*CB=\frac{1}{2}*\frac{4}{5}*45*\frac{1}{ \sqrt{41}} = \frac{18}{\sqrt{41}}$$Ответ: площадь \(S_{ABC} = \frac{18}{\sqrt{41}}\)



