Рассмотрим рисунок
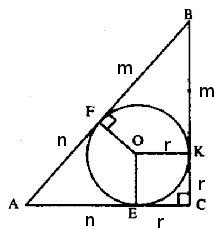
Используя теорему Пифагора и формулу площади прямоугольного треугольника, получили систему уравнений: $$\begin{cases}(r+n)^2+(r+m)^2 = (m+n)^2\\ S = \frac{1}{2}(m+r)(n+r)\end{cases} =>\begin{cases} r^2 + 2rn +n^2+ r^2 + 2rm+m^2 = m^2+2mn+n^2\\ S = \frac{1}{2}(mn+mr+rn+r^2)\end{cases} =>$$$$\begin{cases} 2r^2 + 2rn + 2rm = 2mn\\ S = \frac{1}{2}(mn+mr+rn+r^2)\end{cases} =>\begin{cases} r^2 + rn + rm = mn\\ S = \frac{1}{2}(mn+mr+rn+r^2)\end{cases} =>$$подставляем первое уравнение во второе $$\begin{cases} r^2 + rn + rm = mn\\ S = \frac{1}{2}(mn+mn)\end{cases} =>\begin{cases} r^2 + rn + rm = mn\\ S = mn\end{cases} =>$$Ответ: площадь прямоугольного треугольника равна \(S_{ABC} = mn\)





