Решение:
Областью определения функции двух переменных \(z=f(x;y)\) называется множество всех пар \((x;y)\), т.е. все точки плоскости XOY, для которых существует значение \(z\).
Найдем область определения функции \(z = \frac{1}{x} + \frac{1}{y}\). При нахождении области определения рассмотрим две дроби \(\frac{1}{x};\frac{1}{y}\) . Для дробей область определения - знаменатель дроби не равен нулю, т.е. получили область определения функции двух переменных $$D_f = \begin{cases} x \ne 0\\ y \ne 0\end{cases}$$ Получили, что областью определения функции являются все точки декартовой системы координат кроме точек, принадлежащих осям.
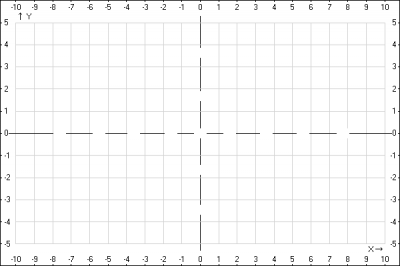
Построим область определения на плоскости XOY . На плоскости \(x=0\) и \(y=0\) - прямые, оси системы координат. Т.к. эти прямые не входят в область определения функции, то мы их изображаем пунктирными линиями.