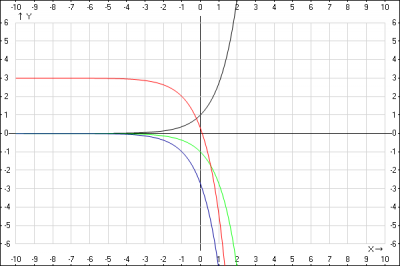
Решение: построим график функции \(y = 3 - e^{x+1}\) путем элементарных преобразований
Порядок построения графика функции.
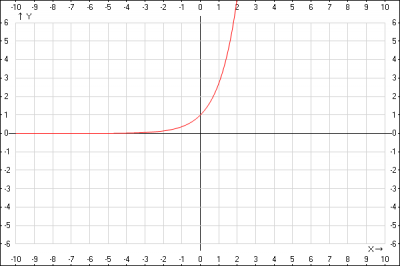
1. строим график элементарной функции \(y = e^x\)
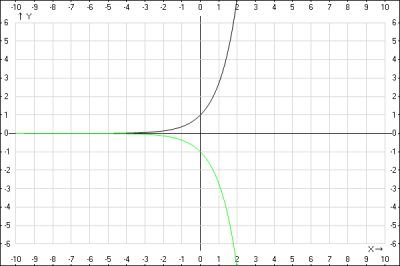
2. строим график функции \(y = -e^x\)
нам нужно построить график функции \(y = -f(x)\).
Для того, чтобы построить график функции \(y = -f(x)\), нужно построить изображение, симметричное графику функции \(y = f(x)\) относительно от абсцисс (Ox).
Строим график функции \(y = -e^{x}\) как симметричное отображение кривой \(y = e^{x}\) относительно оси Ox
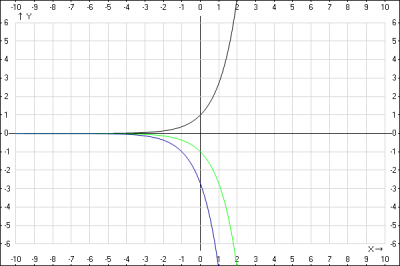
3. строим график функции \(y = -e^{x+1}\)
Для того, чтобы построить график функции \(y = f(x+a)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси абсцисс (Ox) на \(a\) единиц, если \(a > 0 \) влево и если \(a < 0 \) вправо.
График функции \(y = - e^{x}\) переносим на 1 влево, получаем график функции \(y = - e^{x}\)
4. строим график функции \(y = 3-e^{x+1}\)
Для того, чтобы построить график функции \(y = a+ f(x)\), нужно кривую \(y = f(x)\) сдвинуть без деформации вдоль оси ординат (Oy) на \(a\) единиц, если \(a > 0 \) вверх и если \(a < 0 \) вниз.
График функции \(y = - e^{x+1}\) переносим на 3 вверх вдоль оси Oy, получаем график функции \(y = 3 - e^{x}\)