Рассмотрим рисунок
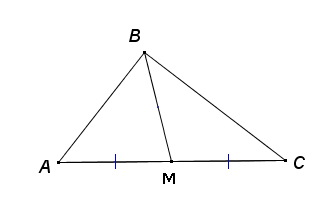
Отрезок, соединяющий вершину \(B \)с серединой противоположной стороны - медиана \(BM\). Как известно, медиана делит треугольник на два равновеликих треугольника, т.е.на два равных по площади треугольника (если из вершины опустить высоту то у обоих треугольников высота общая, а стороны, на которые опущена высота одинаковые, поэтому площадь одинаковая). Обозначим за \(AC = 2x => AM=MC=x\) Для решения задачи воспользуемся формулой площади через полупериметр $$S = \sqrt{p*(p-a)(p-b)(p-c)}$$где \(p = \frac{a+b+c}{2}\). Так как у треугольников \(S_{ABM}=S_{MBC}\). Рассчитаем площадь \(ΔABM\) \(P_{ΔABM} =\frac{13+4+x}{2}\), $$S_{ΔABM}=\sqrt{\frac{13+4+x}{2}*\frac{13+4+x-2*13}{2}*\frac{13+4+x-2*4}{2}*\frac{13+4+x-2*x}{2}}=$$$$=\sqrt{ \frac{17+x}{2}*\frac{x-9}{2}*\frac{9+x}{2}*\frac{17-x}{2}}$$Тоже сделаем и для \(ΔBMС\) \(P_{ΔBMС} =\frac{7+4+x}{2}\),
$$S_{ΔBMС}=\sqrt{ \frac{7+4+x}{2}*\frac{7+4+x-2*7}{2}*\frac{7+4+x-2*4}{2}*\frac{7+4+x-2*x}{2}}=$$$$= \sqrt{\frac{11+x}{2}*\frac{x-3}{2}*\frac{3+x}{2}*\frac{11-x}{2}}$$Приравняем две площади и найдем \(x\) $$S_{ΔABM}= S_{ΔBMС} =>$$
$$\sqrt{ \frac{17+x}{2}*\frac{x-9}{2}*\frac{9+x}{2}*\frac{17-x}{2}}=\sqrt{ \frac{11+x}{2}*\frac{x-3}{2}*\frac{3+x}{2}*\frac{11-x}{2}} =>$$
$$(17+x)(x-9)(9+x)(17-x)=(11+x)(x-3)(3+x)(11-x) =>$$$$(17^2-x^2)(x^2-9^2)=(x^2-3^2)(11^2-x^2) =>$$$$17^2*x^2-17^2*9^2-x^2*x^2 +9^2*x^2=11^2*x^2-x^4-3^2*11^2+3^2*x^2 =>$$$$ 22320 = 240x^2 =>93 = x^2 =>x=\sqrt{93}$$ Получили \(AC = 2*AM = 2*\sqrt{93}\). Используем ту же формулу для нахождения площади всего треугольника \(P_{ABC}=\frac{13+7+2*\sqrt{93}}{2} = 10+\sqrt{93}\). Рассчитаем площадь $$S_{ABC} = \sqrt{(10+\sqrt{93})(10+\sqrt{93}-13)(10+\sqrt{93}-7)(10+\sqrt{93}-2*\sqrt{93})} =$$$$= \sqrt{(10+\sqrt{93})(\sqrt{93}-3)(3+\sqrt{93})(10-\sqrt{93})}=>$$$$ \sqrt{(100-93)(93-9)}=\sqrt{7*84}=14\sqrt{3}$$ Ответ площадь треугольника равна \(S_{ABC} =14\sqrt{3}\)









