Тело соскальзывает без трения с наклонной плоскости.

Решение: тело соскальзывает по плоскости без трения. Рассмотрим рисунок

 

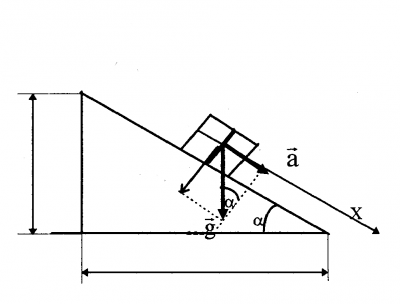
Тело соскальзывает под действием силы тяжести с ускорением $a$. Из рисунка получим связь между ускорением свободного падения $g$ и ускорением соскальзывания $a$, получаем

$$a = g\sin\alpha$$ Из задания следует, что нам нужно найти угол $\alpha$.
В условии задачи говорится о двух средних скоростях $v_1{ср}$ и  $v_2{ср}$. Как известно, средняя скорость при равноускоренном движении рассчитывается как среднеарифметическое скорости в начале и конце пути, т.е. $v_{ср} = \frac{v_1+v_2}{2}$. Согласно условия задачи тело соскальзывает, т.е. начальная скорость $v_0 = 0$, скорость движения тела через $t_1 = 0.5 сек$ равна $v_1 = at_1$, тогда средняя скорость на этом участке равна $$v_1{ср} =  \frac{0+at_1}{2} = \frac{at_1}{2}$$ аналогично получаем и для интервала $t_2 = 1,5 с$  $$v_2{ср} =\frac{at_2}{2}$$ согласно условия задачи первая средняя скорость на $2,5\frac{м}{с}$ меньше, чем вторая, т.е. $$v_1{ср} + 2,5 = v_2{ср} => \frac{at_1}{2} + 2,5 = \frac{at_1}{2}$$ подставляем известные данные $$\frac{a*0,5}{2} + 2,5 = \frac{a*1,5}{2} =>\frac{a}{2} = 2,5 => a = 5$$ Подставляем выражение $a = g\sin\alpha$, получаем $$g\sin\alpha = 5 => \sin\alpha = \frac{5}{g} = \frac{1}{2} => \alpha = 30^0$$
Ответ: угол наклона плоскости к горизонту равен $\alpha = 30^0$