Решение: рассмотрим рисунок.
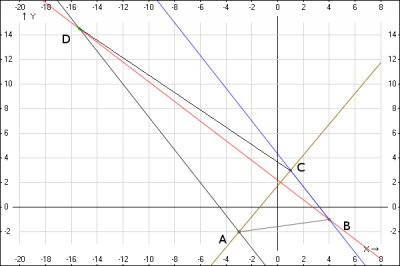
Из рисунка видно, что координату точки D можно найти как точку пересечения двух прямых. Выберем эту пару прямых.
1. Прямая CD - для этой прямой известна только координата одной точки - C.
2. Прямая AD - для этой прямой известна координата одной точки A и направление - прямая AD параллельна прямой BC \(AD||BC\), а для прямой BC - известны координаты двух точек B и C, т.е можно построить прямую по двум точкам.
3. Прямая BD - для этой прямой известна координата одной точки B и направление - прямая BD перпендикулярна прямой AC \(BD \perp AC\), а для прямой AC - известны координаты двух точек A и C, т.е можно построить прямую по двум точкам.
Из приведенного выше анализа приходим к выводу, что координаты точки D будем искать как точку пересечение двух прямых AD и BD.
1. Найдем уравнение прямой AD.
Даны координаты вершины A(-3;-2) и сказано, что прямая \(AD||BC\).
Уравнение прямой AD будем искать, используя уравнение прямой проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x - x_0) \quad (1)$$ Угловые коэффициент прямых \(k_{AD} = k_{BC}\), как угловые коэффициенты двух параллельных прямых.
Найдем уравнение прямой BC. Известны координаты двух точек этой прямой В(4;-1), С(1;3), поэтому уравнения прямой BC будем искать как уравнение прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \quad (2) \) Подставляем координаты вершин: $$BC: \quad \frac{x-4}{1-4} = \frac{y+1}{3+1} => y = \frac{13}{3} - \frac{4}{3}x$$ Из уравнения прямой получаем угловой коэффициент \(k_{BC} = -\frac{4}{3} => k_{AD} = -\frac{4}{3}\)
Найдем уравнение прямой AD, подставим координаты вершину A(-3;-2) и угловой коэффициент \(k_{AD} = -\frac{4}{3}\) в уравнение (1) $$AD: \quad y +2 = -\frac{4}{3}(x - 3) => y = -6 - \frac{4}{3}x$$
2. Найдем уравнение прямой BD.
Даны координаты вершины В(4;-1) и сказано, что прямая \(BD \perp AC\).
Уравнение прямой BD будем искать, используя уравнение прямой проходящей через заданную точку в заданном направлении $$ y - y_0 = k(x - x_0) \quad (1)$$ Угловой коэффициент прямых \(k_{AC} =-\frac{1}{k_{BD}}\), как угловые коэффициенты двух перпендикулярных прямых.
Найдем уравнение прямой AC. Известны координаты двух точек этой прямой A(-3;-2), С(1;3), поэтому уравнения прямой будем искать как уравнение прямой, проходящей через две заданные точки \( \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} \) Подставляем координаты вершин: $$AC: \quad \frac{x+3}{1+3} = \frac{y+2}{3+2} => y = \frac{7}{4} + \frac{5}{4}x$$ Из уравнения прямой получаем угловой коэффициент \(k_{AC} = \frac{5}{4} => k_{BD} = -\frac{4}{5}\)
Найдем уравнение прямой BD, подставим координаты вершины B(4;-1) и угловой коэффициент \(k_{BD} = -\frac{4}{5}\) в уравнение (1) $$BD: \quad y +1 = -\frac{4}{5}(x - 4) => y = \frac{11}{5} - \frac{4}{5}x$$
3. Найдем точку пересечения двух прямых AD и BD.
Составляем систему уравнений $$\begin{cases}y = -6 - \frac{4}{3}x\\ y= \frac{11}{5} - \frac{4}{5}x\end{cases} => \begin{cases}3y = -18 - 4x\\ 5y= 11 - 4x\end{cases} =>$$$$ \begin{cases}3y = -18 - 4x\\ 5y= 11 - 4x\end{cases} => \begin{cases} y = 14.5\\ x=-15.375 \end{cases}$$
Ответ: координаты искомой вершины \(D(-15.375;14.5)\)



