ABCDEF - правильный шестиугольник. Площадь треугольника АВС равна 12 см кв. Найдите площадь шестиуго

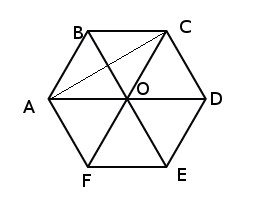
Правильный шестиугольник - это правильный многоугольник с шестью сторонами, т.е. стороны и углы при вершинах равны. Рассмотрим рисунок. Рассмотрим треугольники при вершине О. Все углы при вершине равны между собой и их величина$\frac{360}{6}=60$. ΔABO равнобедренный, а т.к. угол при вершине О равен 60, то два других при основании по  $\frac{180-60}{2} = 60$, т.е. получили что треугольники с вершиной в О - правильные треугольники. Рассмотрим правильные треугольники ΔABO и ΔBCO это правильные треугольники, при этом стороны у них равны (AB=BC т.к. по условию шестиугольник правильный), т.е. ABCO - ромб, а AC и BO - диагонали ромба. Диагональ AC разделила ромб на два равных треугольника т.е. $S_{ABC} = S_{ACO}$ отсюда следует, что площадь ромба равна $S_{ABCO} = 2*S_{ABC} = 24$, в то же время диагональ BO также делит ромб на два равных треугольника, площади которых также равны,т.е. получили, что $S_{ABO} = 12$, т.к. все шесть треугольников при вершине О равносторонние и равные между собой, то площадь шестиугольника