Завдання: на рисунку зображено графік функції \(F(x) = x^2 + bx + c\), яка є первісною для функції \(f(x)\). Визначте параметри b і c, знайдіть функцію \(f(x)\). У відповіді запишіть значення \(f(-8)\).
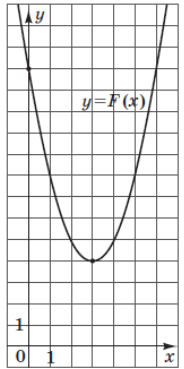
Рішення: в задании нам необходимо найти значение производной функции \(F(x)\) в точке x=-8. Найдем ее $$f(x) = F'(x) = (x^2 + bx + c)' = 2x+b$$В уравнении производной у нас есть неизвестный коэффициент b. Найдем его следующим образом. Вершина параболы c координатами (3;4) (смотреть рисунок) является его точкой экстремума (точка минимума), поэтому в этой точке производная равна 0. Подставим значение x=3 в производную и приравняем ее к 0 и найдем b. $$2x + b = 0 => 2*3 + b = 0 => b = -6$$Подставляем в уравнение производной $$f(x) = 2x -6$$а теперь можно найти значение производной в точке x = -8 $$f(-8) = 2(-8) -6 = -22$$
Відповідь: -22
Рассмотрим другие варианты этой задачи:
2. Завдання: на рисунку зображено графік функції \(F(x) = x^2 + bx + c\), яка є первісною для функції \(f(x)\). Визначте параметри b і c, знайдіть функцію \(f(x)\). У відповіді запишіть значення \(f(-5)\).
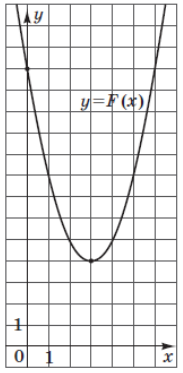
Рішення: $$f(x) = F'(x) = (x^2 + bx + c)' = 2x+b $$ Вершина параболы c координатами (3;4) (смотреть рисунок) является его точкой экстремума (точка минимума), поэтому в этой точке производная равна 0. Подставим значение x=3 в производную и приравняем ее к 0 и найдем b. $$2x + b = 0 => 2*3 + b = 0 => b = -6$$Подставляем в уравнение производной $$f(x) = 2x -6$$а теперь можно найти значение производной в точке x = -8 $$f(-5) = 2(-5) -6 = -16$$
Відповідь: -16
2. Завдання: на рисунку зображено графік функції \(F(x) = x^2 + bx + c\), яка є первісною для функції \(f(x)\). Визначте параметри b і c, знайдіть функцію \(f(x)\). У відповіді запишіть значення \(f(-6)\).

Рішення: $$f(x) = F'(x) = (x^2 + bx + c)' = 2x+b $$ Вершина параболы c координатами (3;4) (смотреть рисунок) является его точкой экстремума (точка минимума), поэтому в этой точке производная равна 0. Подставим значение x=3 в производную и приравняем ее к 0 и найдем b. $$2x + b = 0 => 2*3 + b = 0 => b = -6$$Подставляем в уравнение производной $$f(x) = 2x -6$$а теперь можно найти значение производной в точке x = -6 $$f(-5) = 2(-6) -6 = -18$$
Відповідь: -18

