ЗНО 2013 року з математики (2 сесія). Завдання № 33.

Завдання: при якому найбільшому від'ємному значенні параметра $a$ рівняння $\sqrt[4]{|x| - 1} - 2x = a$ має один корінь?

Рішення: метод решения данной задачи указан в самом задании: "при якому найбільшому від'ємному значенні параметра $a$ рівняння має один корінь", т.е. непосредственно в задании есть подсказка на нахождение функциональной зависимости $a(x)$. Вторая подсказка - найти наибольшее значение, т.е. это прямо указывает на нахождение экстремума (максимума) функциональной зависимости $a(x)$. Ну и последняя подсказка - как решить вопрос с модулем. В задании сказано, что $a$ - отрицательное. Рассмотрим равенство $(\sqrt[4]{|x| - 1} - 2x = a$, область значений $E_{\sqrt[4]{|x| - 1}} =[0; +\infty)$, т.е. этот член (уменьшаемое) всегда положительный, а второй член (вычитаемое) $2x$ должен быть всегда положительным, чтобы разность $a$ была отрицательная. Получили, что зависимость  $a(x)$ рассматривается только при $x >0$. Сразу же запишем ОДЗ корня $|x| - 1 \geq 0 => |x| \geq 1 => x \in (-\infty -1] \cup [1;+\infty)$. Вывод при нахождении точка максимума $x \in [1;+\infty)$.Теперь можно раскрыть модуль

$$\sqrt[4]{x - 1} - 2x = a$$ Необходимым условием существования экстремума является равенство 0 первой производной. Находим производную и приравняем ее к 0 $a'(x) =0$. $$a' = (\sqrt[4]{x - 1} - 2x)' = ((x - 1)^{\frac{1}{4}} - 2x)' = \frac{1}{4}(x - 1)^{\frac{1}{4}-1} - 2 = 0  =>(x - 1)^{-\frac{3}{4}} = 8  =>$$ $$(x - 1)^{\frac{3}{4}} = (\frac{1}{2})^3  =>(x - 1)^{\frac{1}{4}} = \frac{1}{2} =>$$ возведем в 4 степень обе стороны равенства $$( (x - 1)^{\frac{1}{4}})^4 = (\frac{1}{2})^4 =>  x - 1 = \frac{1}{16} => x = \frac{17}{16}$$ Мы нашли, что на заданном интервале есть стационарная (критическая) точка (точка максимума, минимума или точка перегиба). Однако, сделать вывод , что в данной точке есть точка максимума можно лишь на основании дополнительного исследования.  Достаточным условием существования экстремума (точки максимума) является изменение знака производной при переходе через заданную точку слева с "+" на право на "-". Проверяем, возьмем две точки слева и справа от критической и найдем знак производной

1. Слева от критической точки $x = 1+(0,1)^4$ получаем $a'(1+(0,1)^4) = \frac{1}{4(1+(0,1)^4 - 1)^{-\frac{3}{4}}} - 2 =  \frac{1}{4(0,1)^{3}} - 2 =  \frac{10^3}{4} - 2 > 0$
2. Справа от критической точки $x = 2$ получаем $a'(2) = \frac{1}{4(2 - 1)^{-\frac{3}{4}}} - 2 =  \frac{1}{4} - 2 <  0$   
Знак производной поменялся с "+" на  "-", т.е. это точка максимума. Также можно сделать вывод, что слева от точки максимума функция возрастает, а справа убывает, т.е. эта точка является еще и наибольшим значением на интервале $x \in [1; +\infty)$, т.е. это та точка которую мы ищем.

Теперь осталось подставить полученное значение $x$  в уравнение и найти значение функции $a(x)$

$$a( \frac{17}{16}) = \sqrt[4]{x - 1} - 2x = \sqrt[4]{ \frac{17}{16}- 1} - 2*\frac{17}{16} = \sqrt[4]{ \frac{1}{16}} -  \frac{17}{8} = \frac{1}{2} - \frac{17}{8} = -\frac{13}{8} = -1,625$$ В качестве графического доказательства правильности решения задания на рисунке я построил зависимость $a(x) = \sqrt[4]{|x| - 1} - 2x$

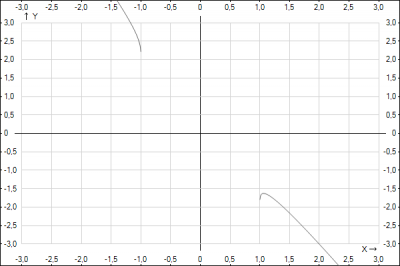
 Відповідь: -1,625

Рассмотрим другие варианты этой задачи:

2. Завдання: при якому найбільшому від'ємному значенні параметра $a$ рівняння $\sqrt[4]{|x| - 2} - 2x = a$ має один корінь?

Рішення:

$$a(x) = \sqrt[4]{x - 2} - 2x$$ $$a'(x) = (\sqrt[4]{x - 2} - 2x)' = \frac{1}{4}*(x-2)^{-\frac{3}{4}} -2 =0 => (x - 2)^{-\frac{3}{4}} = 8  =>$$ $$(x - 2)^{\frac{3}{4}} = (\frac{1}{2})^3  =>(x - 2)^{\frac{1}{4}} = \frac{1}{2} =>$$ возведем в 4 степень обе стороны равенства $$( (x - 2)^{\frac{1}{4}})^4 = (\frac{1}{2})^4 =>  x - 2 = \frac{1}{16} => x = \frac{33}{16}$$ Подставим полученное значение $x$  в уравнение и найти значение функции $a(x)$ $$a( \frac{33}{16}) = \sqrt[4]{x - 2} - 2x = \sqrt[4]{ \frac{33}{16}- 2} - 2*\frac{33}{16} = \sqrt[4]{ \frac{1}{16}} -  \frac{33}{8} = \frac{1}{2} - \frac{33}{8} = -\frac{29}{8} = -1,625$$ График функции $a(x) =\sqrt[4]{|x| - 2} - 2x$

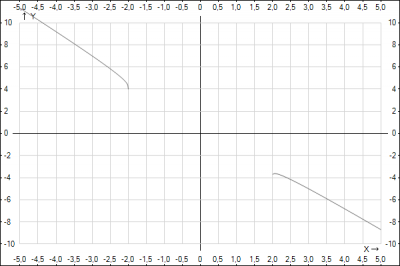
Відповідь: -3,625

3. Завдання: при якому найбільшому від'ємному значенні параметра $a$ рівняння $\sqrt[4]{|x| - 3} - 2x = a$ має один корінь?

Рішення:

$$a(x) = \sqrt[4]{x - 3} - 2x$$ $$a'(x) = (\sqrt[4]{x - 3} - 2x)' = \frac{1}{4}*(x-3)^{-\frac{3}{4}} -2 =0 => (x - 3)^{-\frac{3}{4}} = 8  =>$$ $$(x - 3)^{\frac{3}{4}} = (\frac{1}{2})^3  =>(x - 3)^{\frac{1}{4}} = \frac{1}{2} =>$$ возведем в 4 степень обе стороны равенства $$( (x - 3)^{\frac{1}{4}})^4 = (\frac{1}{2})^4 =>  x - 3 = \frac{1}{16} => x = \frac{49}{16}$$ Подставим полученное значение $x$  в уравнение и найти значение функции $a(x)$ $$a( \frac{49}{16}) = \sqrt[4]{x - 3} - 2x = \sqrt[4]{ \frac{49}{16}- 3} - 2*\frac{49}{16} = \sqrt[4]{ \frac{1}{16}} -  \frac{49}{8} = \frac{1}{2} - \frac{49}{8} = -\frac{45}{8} = -5,625$$ График функции $a(x) =\sqrt[4]{|x| - 3} - 2x$

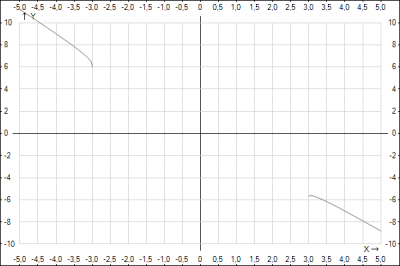
Відповідь: -5,625

попереднє завдання № 32