–Ч–∞–≤–і–∞–љ–љ—П: –њ–ї–∞–љ –њ–∞—А–Ї–Њ–≤–Њ—Ч –Ј–Њ–љ–Є, –Њ–±–Љ–µ–ґ–µ–љ–Њ—Ч —В—А–Є–Ї—Г—В–љ–Є–Ї–Њ–Љ ABC, –Ј–Њ–±—А–∞–ґ–µ–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї—Г. –Ф—Г–≥–∞ AB вАУ –≤–µ–ї–Њ—Б–Є–њ–µ–і–љ–∞ –і–Њ—А—Ц–ґ–Ї–∞. –Т—Ц–і–Њ–Љ–Њ, —Й–Њ –і—Г–≥–∞ AB —Ф —З–µ—В–≤–µ—А—В–Њ—О —З–∞—Б—В–Є–љ–Њ—О –Ї–Њ–ї–∞ —А–∞–і—Ц—Г—Б–∞ 1,8 –Ї–Љ. CA —Ц CB вАУ –і–Њ—В–Є—З–љ—Ц –і–Њ —Ж—М–Њ–≥–Њ –Ї–Њ–ї–∞ (A —Ц B вАУ —В–Њ—З–Ї–Є –і–Њ—В–Є–Ї—Г). –Ю–±—З–Є—Б–ї—Ц—В—М –њ–ї–Њ—Й—Г –Ј–Њ–±—А–∞–ґ–µ–љ–Њ—Ч –њ–∞—А–Ї–Њ–≤–Њ—Ч –Ј–Њ–љ–Є (—Г \(–Ї–Љ^2\)).
 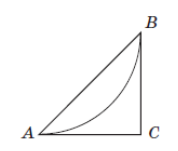
–†—Ц—И–µ–љ–љ—П: –≤ –Ј–∞–і–∞–љ–Є–Є –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –љ–∞–є—В–Є –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ќФABC. –Ф–Њ—А–Є—Б—Г–µ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —А–Є—Б—Г–љ–Њ–Ї. –†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї OBCA. –Ъ–∞–Ї –Є–Ј–≤–µ—Б—В–љ–Њ, —А–∞–і–Є—Г—Б, –Њ–њ—Г—Й–µ–љ–љ—Л–є –≤ —В–Њ—З–Ї—Г –Ї–∞—Б–∞–љ–Є—П –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ–љ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є. –Ґ.–Њ. –≤—Б–µ —Г–≥–ї—Л —Г —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –њ—А—П–Љ—Л–µ, –∞ —Б—В–Њ—А–Њ–љ—Л —А–∞–≤–љ—Л –Є —А–∞–≤–љ—Л R, —В.–µ. —Н—В–Њ—В —З–µ—В—Л—А–µ—Е —Г–≥–Њ–ї—М–љ–Є–Ї - –Ї–≤–∞–і—А–∞—В. –°—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ \(BC =OA = R, AC = OB = R\). –Я–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –±—Г–і–µ—В —А–∞–≤–љ–∞ \(S_{ќФABC} =\frac{1}{2}AC*BC = \frac{1}{2}R^2\) –њ–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –Ј–љ–∞—З–µ–љ–Є–µ —А–∞–і–Є—Г—Б–∞ –Є –њ–Њ–ї—Г—З–∞–µ–Љ¬† \(S_{ќФABC} = \frac{1}{2}R^2 = \frac{1}{2}1,8^2 = 1,62 km^2\)
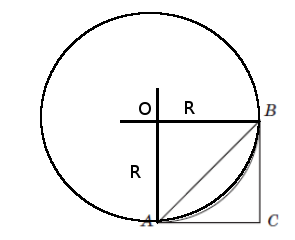
–Т—Ц–і–њ–Њ–≤—Ц–і—М:¬† 1,62
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –і—А—Г–≥–Є–µ –≤–∞—А–Є–∞–љ—В—Л —Н—В–Њ–є –Ј–∞–і–∞—З–Є:
2. –Ч–∞–≤–і–∞–љ–љ—П: –њ–ї–∞–љ –њ–∞—А–Ї–Њ–≤–Њ—Ч –Ј–Њ–љ–Є, –Њ–±–Љ–µ–ґ–µ–љ–Њ—Ч —В—А–Є–Ї—Г—В–љ–Є–Ї–Њ–Љ ABC, –Ј–Њ–±—А–∞–ґ–µ–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї—Г. –Ф—Г–≥–∞ AB вАУ –≤–µ–ї–Њ—Б–Є–њ–µ–і–љ–∞ –і–Њ—А—Ц–ґ–Ї–∞. –Т—Ц–і–Њ–Љ–Њ, —Й–Њ –і—Г–≥–∞ AB —Ф —З–µ—В–≤–µ—А—В–Њ—О —З–∞—Б—В–Є–љ–Њ—О –Ї–Њ–ї–∞ —А–∞–і—Ц—Г—Б–∞ 1,6 –Ї–Љ. CA —Ц CB вАУ –і–Њ—В–Є—З–љ—Ц –і–Њ —Ж—М–Њ–≥–Њ –Ї–Њ–ї–∞ (A —Ц B вАУ —В–Њ—З–Ї–Є –і–Њ—В–Є–Ї—Г). –Ю–±—З–Є—Б–ї—Ц—В—М –њ–ї–Њ—Й—Г –Ј–Њ–±—А–∞–ґ–µ–љ–Њ—Ч –њ–∞—А–Ї–Њ–≤–Њ—Ч –Ј–Њ–љ–Є (—Г \(–Ї–Љ^2\)).
–†—Ц—И–µ–љ–љ—П: \(S_{ќФABC} =\frac{1}{2}AC*BC = \frac{1}{2}R^2 = \frac{1}{2}*1,6^2 = 1,28\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М:¬† 1,28
3. –Ч–∞–≤–і–∞–љ–љ—П: –њ–ї–∞–љ –њ–∞—А–Ї–Њ–≤–Њ—Ч –Ј–Њ–љ–Є, –Њ–±–Љ–µ–ґ–µ–љ–Њ—Ч —В—А–Є–Ї—Г—В–љ–Є–Ї–Њ–Љ ABC, –Ј–Њ–±—А–∞–ґ–µ–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї—Г. –Ф—Г–≥–∞ AB вАУ –≤–µ–ї–Њ—Б–Є–њ–µ–і–љ–∞ –і–Њ—А—Ц–ґ–Ї–∞. –Т—Ц–і–Њ–Љ–Њ, —Й–Њ –і—Г–≥–∞ AB —Ф —З–µ—В–≤–µ—А—В–Њ—О —З–∞—Б—В–Є–љ–Њ—О –Ї–Њ–ї–∞ —А–∞–і—Ц—Г—Б–∞ 1,4 –Ї–Љ. CA —Ц CB вАУ –і–Њ—В–Є—З–љ—Ц –і–Њ —Ж—М–Њ–≥–Њ –Ї–Њ–ї–∞ (A —Ц B вАУ —В–Њ—З–Ї–Є –і–Њ—В–Є–Ї—Г). –Ю–±—З–Є—Б–ї—Ц—В—М –њ–ї–Њ—Й—Г –Ј–Њ–±—А–∞–ґ–µ–љ–Њ—Ч –њ–∞—А–Ї–Њ–≤–Њ—Ч –Ј–Њ–љ–Є (—Г \(–Ї–Љ^2\)).
–†—Ц—И–µ–љ–љ—П: \(S_{ќФABC} =\frac{1}{2}AC*BC = \frac{1}{2}R^2 = \frac{1}{2}*1,4^2 = 0,98\)
–Т—Ц–і–њ–Њ–≤—Ц–і—М:¬† 0,98
¬†–њ–Њ–њ–µ—А–µ–і–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П вДЦ 29 ¬†¬†¬† –љ–∞—Б—В—Г–њ–љ–µ –Ј–∞–≤–і–∞–љ–љ—П вДЦ 31

